Помогите пожалуйста! тема Касательная к окружности

Ответы
Пошаговое объяснение:
43)
1)
∠ОАС=90°; АС- касательная.
∠АСО=∠АСВ/2=76°/2=38° ОС- биссектриса угла ∠АСВ.
∠АОС=90°-∠АСО=90°-38°=52° (сумма острых углов в прямоугольном треугольнике равна 90°; ∆АСО- прямоугольный треугольник.
∆АСО=∆ВСО, по катету и гипотенузе (АО=ОВ,радиусы; ОС- общая гипотенуза)
В равных треугольниках соответственные углы равны.
∠СОВ=∠СОА=52°
∠АСО=∠ВСО=38°
Ответ: ∠ОАС=90°; ∠АСО=38°; ∠АОС=52°; ∠ОВС=90°; ∠ОСВ=38°; ∠СОВ=52°
_____________
2)
D=8см; ВС=5,1см.
ОВ=D/2=8/2=4см радиус (R=D/2)
S(∆OBC)=½*OB*BC=½*4*5,1=10,2 см²
∆OBC=∆OAC, площади треугольников равны.
S(AOBC)=2*S(∆OBC)=2*10,2=20,4 см²
Ответ: S(AOBC)=20,4 см²
______________
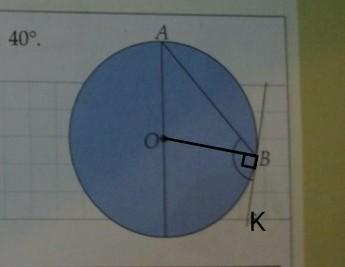
44)
Проведем радиус ОВ.
∠ОВK=90°; BK- касательная
∠ОАВ=∠ОВА=40°, (∆АОВ- равнобедренный, углы при основании равны АО=ОВ, радиусы.)
∠АВК=∠ОВА+∠ОВК=40°+90°=130°
Ответ: угол между касательной s и хордой АВ равен 130°