Предмет: Геометрия,
автор: danigalikasim
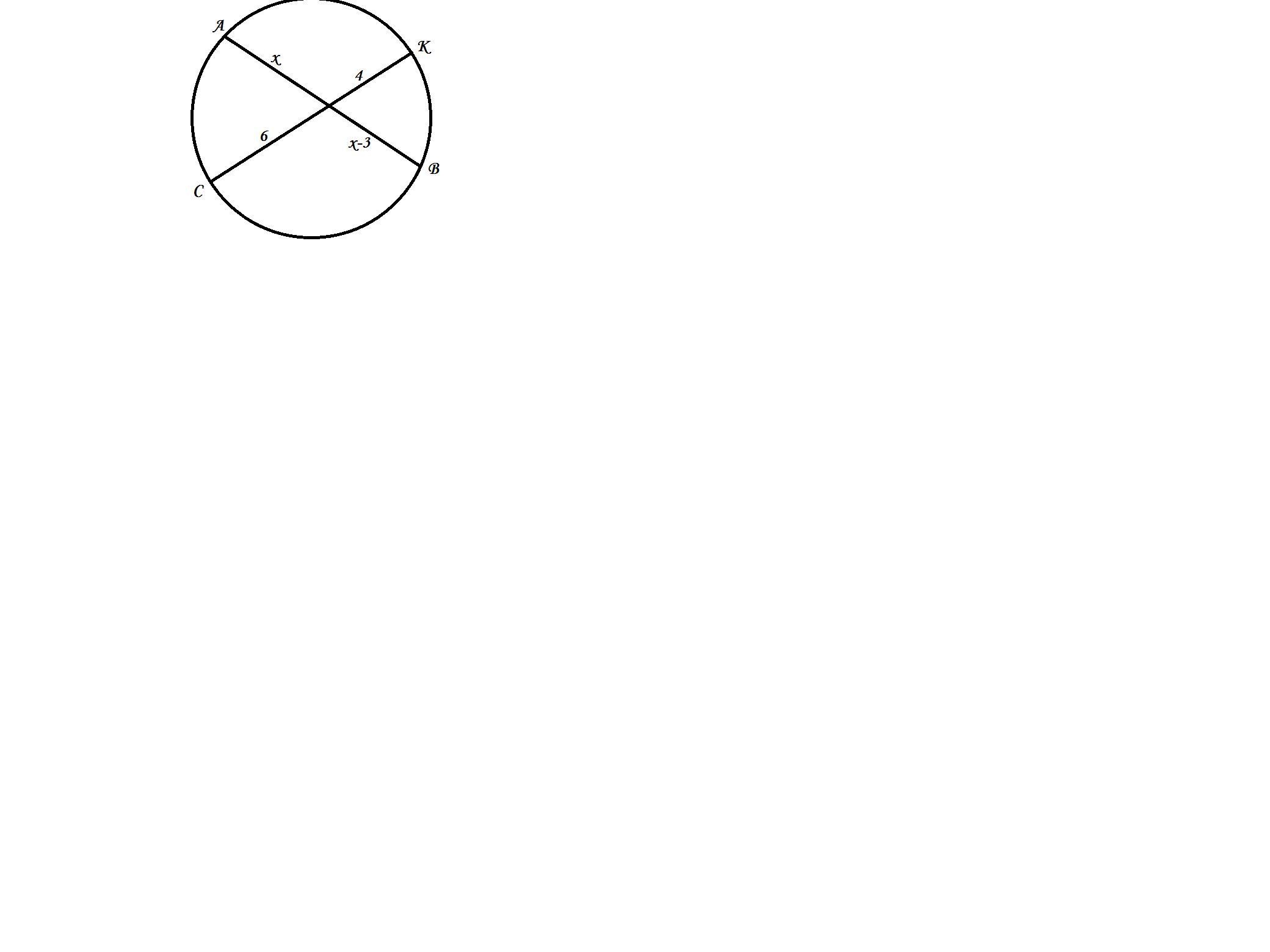
Хорды AB и CK окружности пересекаются в точке E. Вычислите длину отрезка EA, если AE на 3 см больше EB, CE=6см, EK=4 см
Ответы
Автор ответа:
1
Ответ:
По свойству произведения отрезков хорд, получаем:
AE * EB = CE * EK
Заменяем известные значения и находим AE:
AE * (AE - 3) = 6 * 4
AE^2 - 3AE - 24 = 0
Решаем квадратное уравнение:
AE = (3 + sqrt(105))/2 или AE = (3 - sqrt(105))/2
Так как AE должно быть больше EB, то выбираем корень:
AE = (3 + sqrt(105))/2
Ответ: длина отрезка EA равна (3 + sqrt(105))/2 см.
Автор ответа:
0
Ответ:
(3+√105)/2
Объяснение:
Произведения длин отрезков каждой из хорд равны.
ЕА*ЕВ=СЕ*КЕ
Пусть ЕА=х см, тогда ЕВ=х-3 см.
х(х-3)=4*6
х²-3х-24=0
х=(3±√(9+96))/2=(3±√105)/2
х=(3-√105)/2 не подходит; х=(3+√105)/2
АЕ==(3+√105)/2
Приложения:
Похожие вопросы
Предмет: Литература,
автор: lubezaninsasa
Предмет: Другие предметы,
автор: valeriarusanova122
Предмет: Немецкий язык,
автор: kot9paLox
Предмет: Русский язык,
автор: adamoxana182
Предмет: Алгебра,
автор: Fletgii