Предмет: Алгебра,
автор: otkacev056
]. Разность квадратов двух чисел равна 60, а сумма этих чисел равна 15. Найдите эти числа.
Ответы
Автор ответа:
0
Ответ:
Давайте назовем два числа, которые мы хотим найти, "x" и "y".
Из постановки задачи мы знаем, что:
x + y = 15 (уравнение 1)
x^2 - y^2 = 60 (уравнение 2)
Мы можем использовать уравнение 1 для решения для одной из переменных в терминах другой:
y = 15 - x
Теперь мы можем подставить это выражение для y в уравнение 2:
x^2 - (15 - x)^2 = 60
Расширяя квадрат с правой стороны и упрощая, мы получаем:
-30x + 225 = 60
Вычитая 225 с обеих сторон, мы получаем:
-30x = -165
Разделив обе стороны на -30, мы получаем:
x = 5,5
Теперь мы можем использовать уравнение 1, чтобы найти y:
5,5 + y = 15
y = 9,5
Следовательно, эти два числа равны 5.5 и 9.5.
Автор ответа:
1
Решение на прикреплённой фотографии
Приложения:
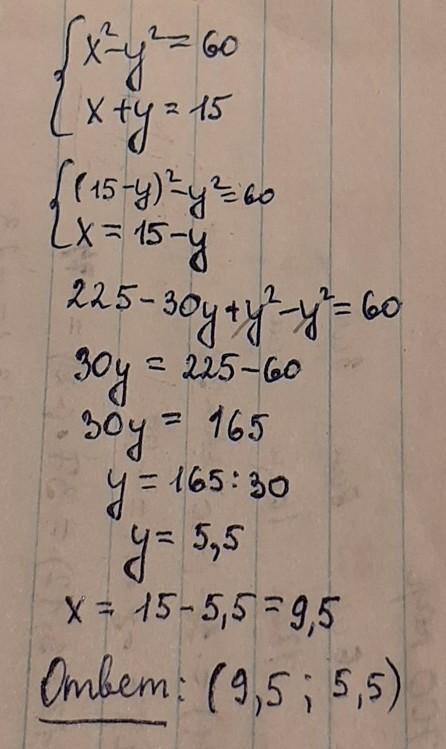
Похожие вопросы
Предмет: Математика,
автор: nastyaD1010
Предмет: Физика,
автор: golubartem2009
Предмет: Физика,
автор: glusenkoanzela6
Предмет: Биология,
автор: FANATEKONA
Предмет: Русский язык,
автор: schavirinatereh