Помогите пожалуйста решить
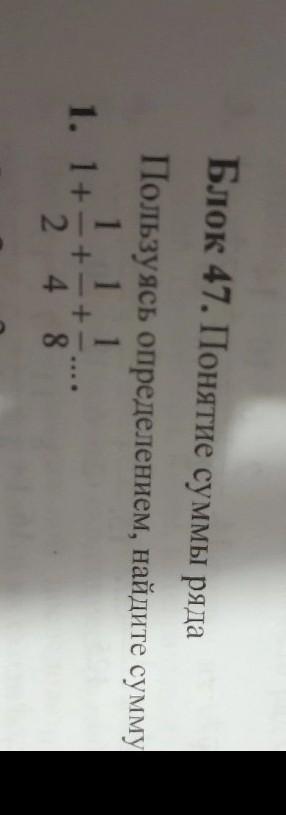
Ответы
Ответ:
2
Объяснение:
Ответ, конечно, 2: представьте, сначала Вы съедаете яблоко (первое слагаемое), затем половину второго (второе слагаемое), затем половину остатка (ведь когда Вы съели половину, у Вас осталасъ несъеденной вторая половина, а четверть яблока - это как раз половина оставшейся половины; при этом у Вас останется четверть яблока), и так далее. В результате бесконечной череды откусываний Вы доедите второе яблоко.
Второй подход - используя школьные знания. Нам же дана бесконечная убывающая геометрическая прогрессия ; |q|<1; её сумма равна
У нас
А теперь найдем сумму исходя из её определения как предела частичных сумм.
Замечаем закономерность:
Докажем её методом математической индукции. При n=1, n=2, n=3 формула верна (хотя достаточно было проверить её при n=1).
Пусть она верна при некотором n=k: докажем, что тогда она верна при n=k+1, то есть что
В самом деле,
Таким образом, методом математитческой индукции гипотеза доказана. Остается найти сумму ряда: