Question

Напишіть розв’язання

Answer 1

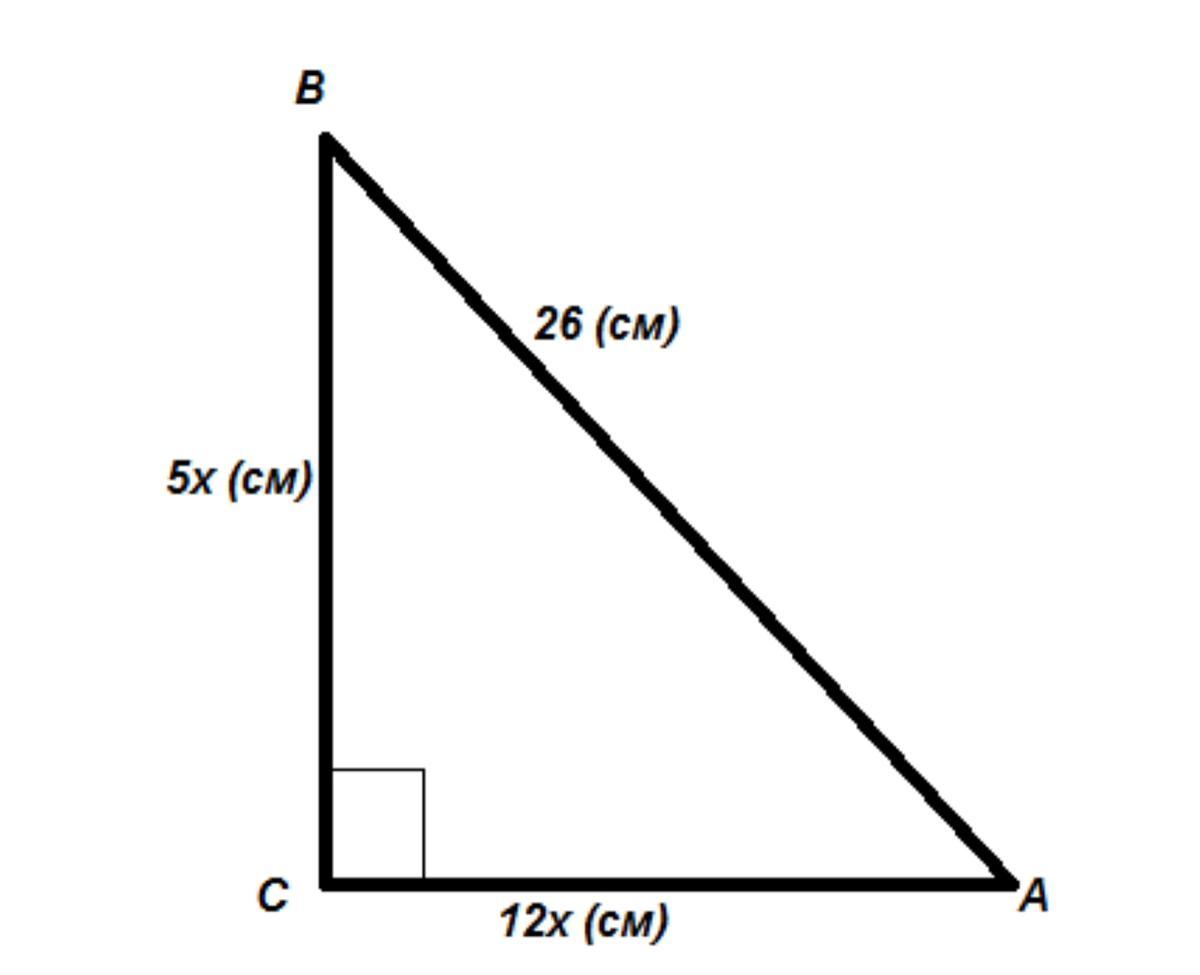
Дано: АВС - прямокутний трикутник; ∠С=90°., АВ = 26см.
Знайти: AC; BC
розв'язання:
Нехай коефіцієнт пропорційності буде х (см), тоді катет ВС - 5х (см), а катет АС - 12 х (см). Гіпотенуза АВ = 26см. За теормею Піфагора складаємо рівняння:
AB^2=BC^2+AC^2
26^2=(5x)^2+(12x)^2
676=25x^2+144x^2
676=169x^2
x^2=676:169
x^2=4
x=2
Отже, коефіцієнт пропорційности х =2. Катети тоді будуть: BC=5x=5•2=10 см и AC = 12x=12•2=24 см.
В-дь: BC=10 см; АС=24 см;