Предмет: Геометрия,
автор: polonskiyvanyok
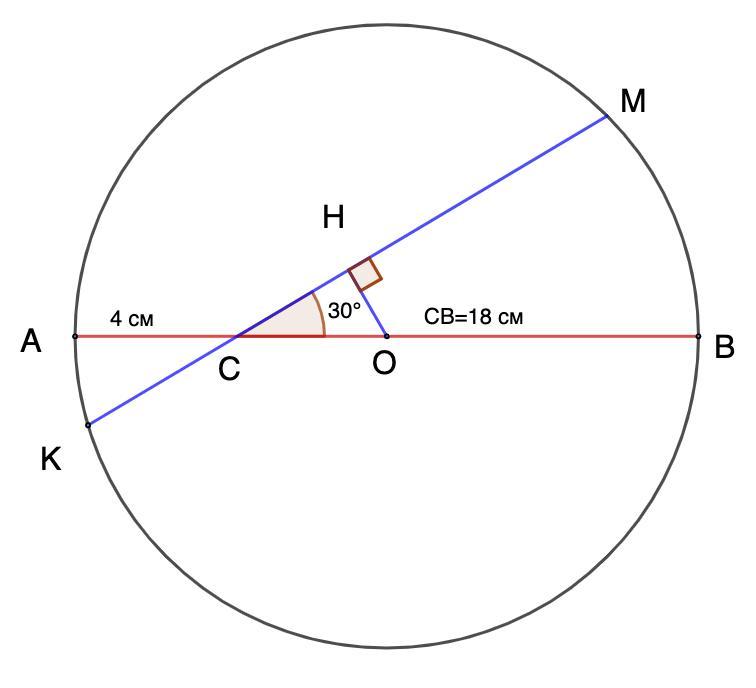
Хорда перетинає діаметр кола під кутом 30° і ділить його на відрізки завдовжки 4 см і 18 см. Знайдіть від- стань від центра кола до цієї хорди.
Ответы
Автор ответа:
15
Ответ:
Расстояние от центра круга до этой хорды равно 3,5 см.
Объяснение:
Хорда пересекает диаметр круга под углом 30° и делит его на отрезки длиной 4 см и 18 см. Найдите расстояние от центра круга до этой хорды.
Дано:
Окр.(О, ОА)
АВ - диаметр, КМ - хорда.
АВ ∩ КМ = С;
АС = 4 см; СВ = 18 см
∠МСВ = 30°
Найти: расстояние от центра круга до этой хорды.
Решение:
- Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.
⇒ ОН - искомый отрезок.
АВ = АС + СВ = 4 + 18 = 22 (см) - диаметр;
- Радиус равен половине диаметра.
⇒ АО = ОВ = 22 : 2 = 11 (см)
СО = ОА - АС = 11 - 4 = 7 (см)
Рассмотрим ΔСНО - прямоугольный.
∠МСВ = 30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ ОН = СО : 2 = 7 : 2 = 3,5 (см)
Расстояние от центра круга до этой хорды равно 3,5 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: zopahahah4
Предмет: Геометрия,
автор: tiktakpenc4
Предмет: Алгебра,
автор: byblic21
Предмет: Математика,
автор: hbro03237
Предмет: География,
автор: fcrnewdawn