Предмет: Геометрия,
автор: izumrudlera1
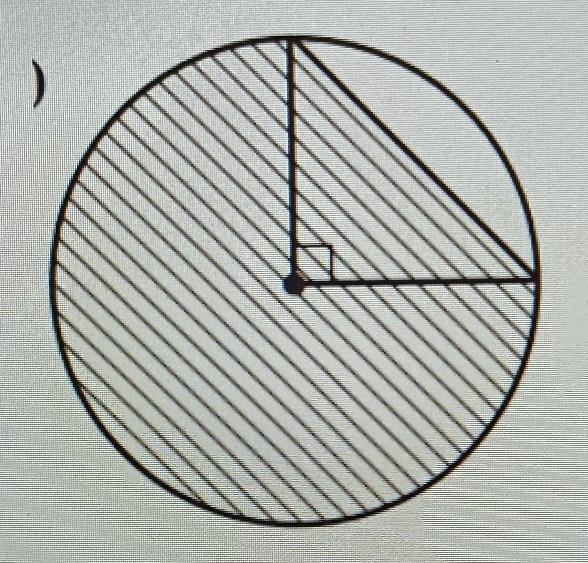
Знайдіть площу заштрихованої фігури, зображеної на рисунку, якщо радіус круга дорівнює 6.
Приложения:
Ответы
Автор ответа:
3
Ответ:
Площадь заштрихованной фигуры равна (27π + 18)ед²
Объяснение:
Не закрашенная часть круга называется сегментом . Чтобы найти площадь заштрихованной части , нужно от площади круга отнять площадь сегмента.
Найдём площадь сегмента по формуле:
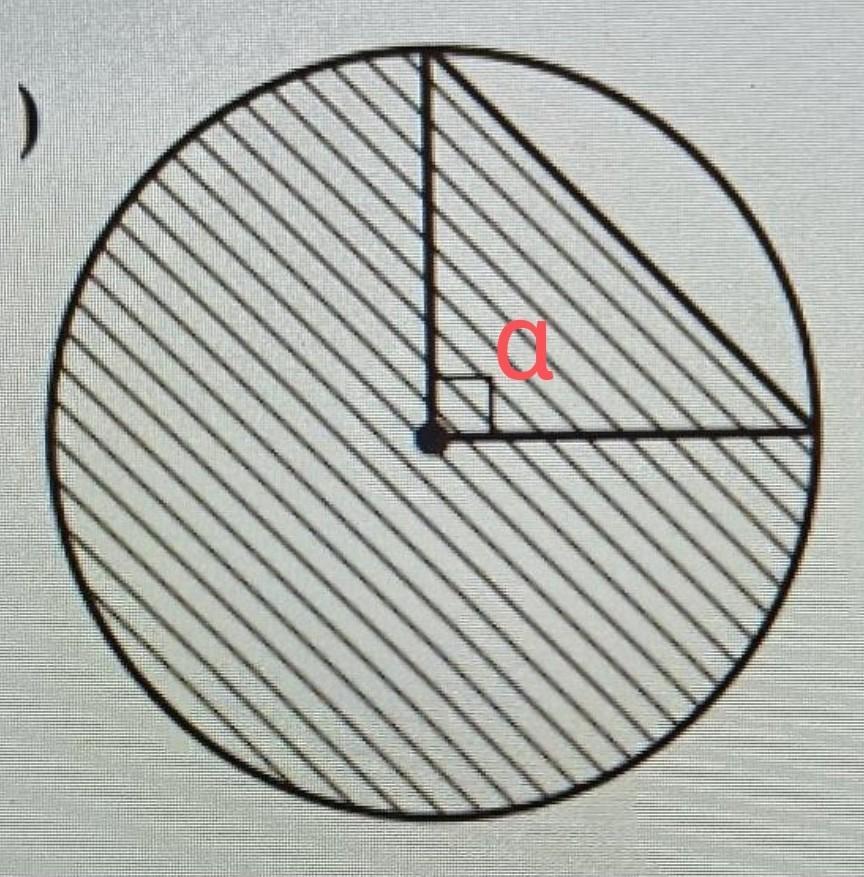
По условию r(радиус) = 6ед , угол α по рисунку прямой , значит , равен 90°(см.вложение)
Находим площадь круга :
Находим площадь заштрихованной фигуры:
Sкр. - Sсег. = 36π - (9π - 18) = (27π + 18)ед²
#SPJ1
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: maksim8964
Предмет: Немецкий язык,
автор: mdkarnaukhov
Предмет: Алгебра,
автор: andrijtrufin16
Предмет: Биология,
автор: Petuhovpetuh326
Предмет: Английский язык,
автор: prettybaby228