Предмет: Геометрия,
автор: olgaryzkova490
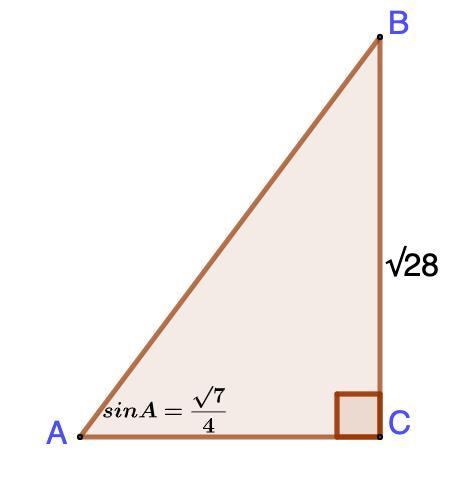
В треугольнике ABC угол C равен 90° , BC=√28 , sin угла A = √7/4.
Найдите AC.
Ответы
Автор ответа:
2
Ответ:
Катет АС равен 6 ед.
Объяснение:
В треугольнике ABC угол C равен 90° , BC=√28 , sinA = √7/4.
Найдите AC.
Дано: ΔАВС - прямоугольный.
∠С = 90°;
ВС = √28; sin A = √7/4
Найти: АС.
Решение:
- Синус угла - отношение противолежащего катета к гипотенузе.
Найдем по теореме Пифагора АС:
АС² = АВ² - ВС² = 64 - 28 = 36 ⇒ АС = √36 = 6
Катет АС равен 6 ед.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: evgeniyaza89
Предмет: Математика,
автор: akhmullayevaguzyal
Предмет: Математика,
автор: ve600941
Предмет: Английский язык,
автор: Касоничка
Предмет: Биология,
автор: mihkataptshka