Question

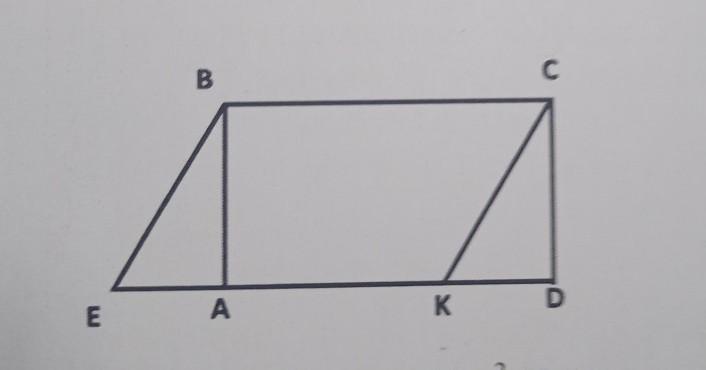
ЗАДАНИЯ 1. Докажите, что прямоугольник АВСД и параллелограмм EBCK, изображенные на рисунке, равновеликие и равносоставленные.​

Answer 1

Ответ:

Равновеликие-это значит,что площадь параллелограмма ЕВСК такая же,как и площадь прямоугольника АВСD

Треугольники АВЕ и КСD равны между собой по 4 признаку равенства прямоугольных треугольников-по катету и гипотенузе

АВ=СD,т к противоположные стороны прямоугольника равны между собой

ЕВ=КС,т к противоположные стороны параллелограмма равны между собой

Равенство треугольников доказано,а значит и

ЕА=КD

Все это доказательство того,что прямоугольник и параллелограмм равносоставленные
S прямоугольника АD•AB

S параллелограмма=ЕК•АВ
Выше было доказано,что

ЕА=КD,значит

ЕК=ЕА+АК=АК+КD=AD, т е

площадь обеих фигур одинаковая

Объяснение: