СРОЧНО ОТДАЮ ВСЕ СВОИ БАЛЛЫ ПОМОГИТЕ ГЕОМЕТРИЯ 9 КЛАСС

Ответы
Объяснение:
2. Б
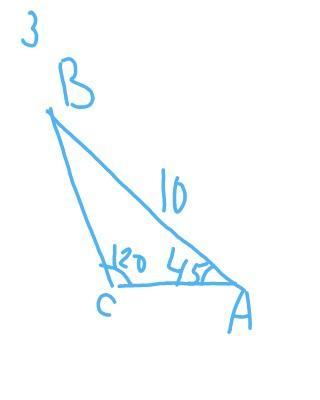
3. на фото
∠В=180-∠А-∠С=180-45-120=15°
из теоремы синусов:
АС/sinB=AB/sinC
AC/sin15=10/sin120
AC=10sin15/sin120
ответ: А
4.
АС=10 см
∠А=∠С=30°
R=AC/sinB
∠B=180-2•∠A=180-2•30=120°
R=10/sin120=10/(√3/2)=20/√3 см
ответ: В
5.
∠В=2•∠МВО=2•30=60° т.к ВО - биссектриса.
∠А=∠С=∠В=60° , значит ∆АВС - равносторонний: АВ=ВС=АС=3 см.
∆МВС - прямоугольный:
по теореме Пифагора:
МС=√(ВС²-ВМ²)
высота МС в прямоугольном тр-ке является медианой : ВМ=АВ:2=3:2=3/2
МС=√(3²-(3/2)²)=√(9-9/4)=
=(√27)/2=(3√3)/2
биссектрисы в равностороннем треугольнике точкой пересечения делятся в соотношении 2:1 начиная от вершины
R=2/3•MC=2/3•(3√3)/2=√3 см
6.
∆АВС: ∠С=150° ; АС=1 см ; ВС=7√3 см
найти: АВ
из теоремы косинусов:
с=√(АС²+ВС²-2•АС•ВС•соsC)=
=√(1²+(7√3)²-2•1•7√3•cos150)=
=√(1+147-14√3•(-√3/2))=
=√(1+147+21)=√169=13 см
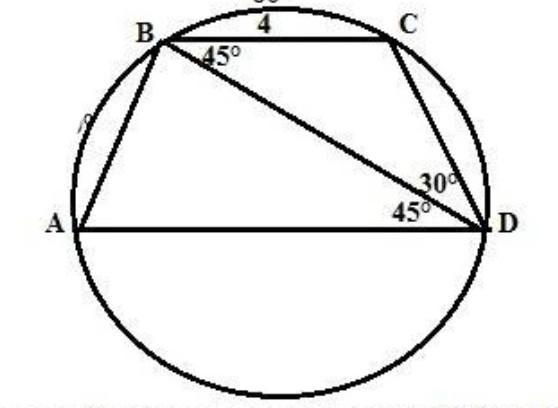
7.на фото
диагональ ВD делит АВСD на
∆АВD=∆CDB.
∠DBC=∠BDA=45° как накрест лежащие при параллельных АD и ВС и секущей ВD.
Радиус окружности,описанной около равнобокой трапеции равен радиусу окружности , описанной вокруг любой из этих треугольников.
R=BC/(2sin∠BDC)=4/(2•sin30)=
=4/(2•1/2)=4 см
по теореме синусов:
СD/sin∠DBC=BC/sin∠BDC
CD/sin45=4/sin30
CD=4•(√2/2):(1/2)=2√2•2=4√2 см
ответ: R=4 см ; СD=4√2 см