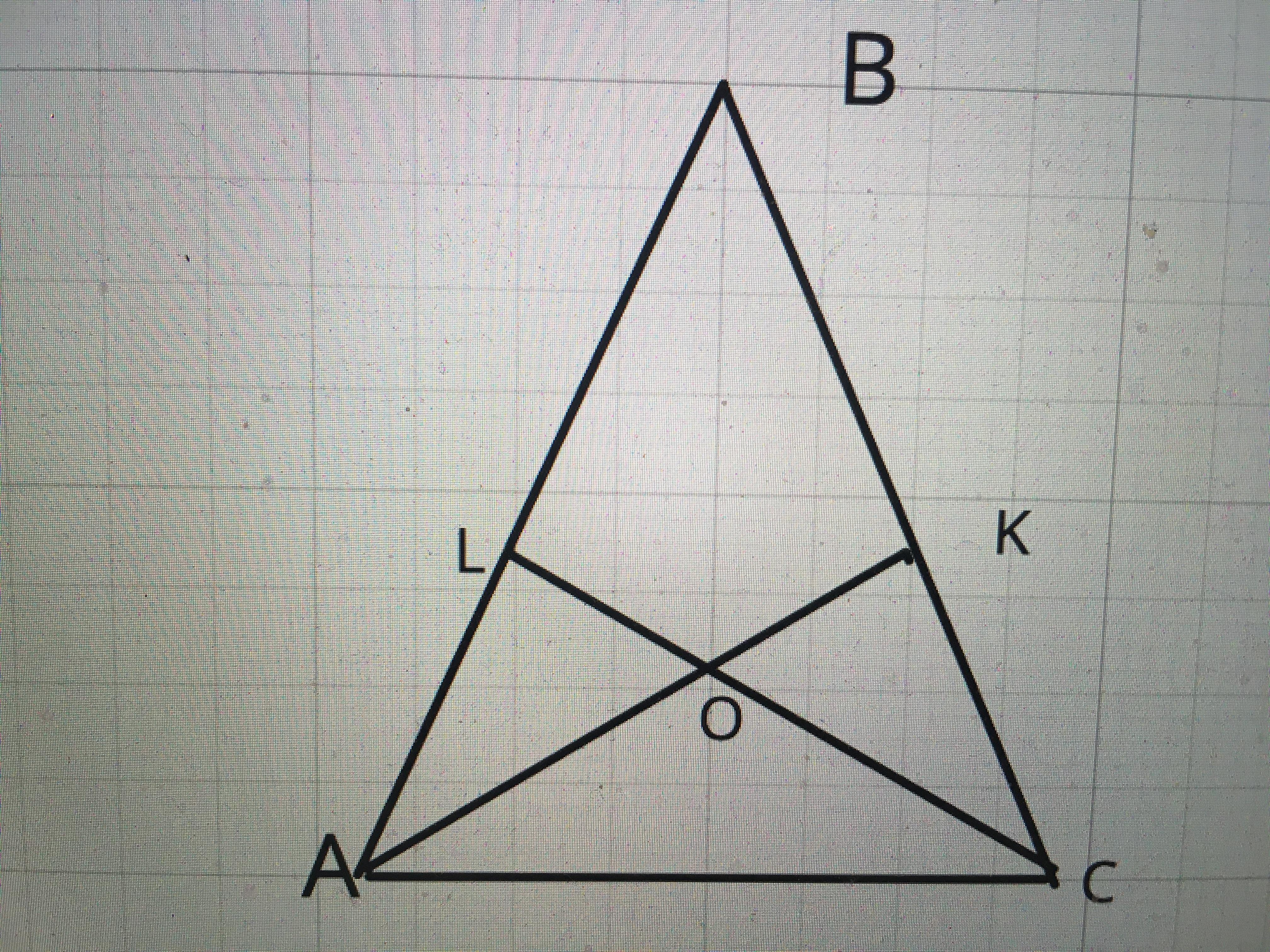
Высота АК и а СL треугольника АВС пересекаются в точке О.АО =СО, АL= ВК. Докажите, что треугольник АВС равносторонний
Ответы
Оскільки АО = СО та АL = ВК, то ми можемо зробити такі спостереження:
1)ОА = ОС, за умовою.
2) ОА = ОL, так як О - це точка перетину висоти АК і CL.
3) ОС = ОК, так як О - це точка перетину висоти АК і CL.
Отже, зі спостережень 1, 2 та 3 випливає, що ОА = ОК та ОС = ОL.
4) Трикутник АОК є рівнобедреним, оскільки ОА = ОК.
5) Трикутник СОЛ є рівнобедреним, оскільки ОС = ОL.
Зі спостережень 4 та 5 випливає, що ОК = АК та ОЛ = СЛ.
Отже, ми маємо наступну систему рівнянь:ОК = АКОЛ = СЛОА = ОС
Звідси випливає, що АК = СЛ, а також ОА = ОК = ОС. Таким чином, всі сторони трикутника АВС мають однакову довжину, тобто трікутник рівносторонній.
Ответ:
Доказано требуемое.
Объяснение:
AO=OC⇒ треугольник AOC равнобедренный, ∠OAC=∠OCA.
Из прямоугольного треугольника AKC ∠ACK=90°-∠KAC; из прямоугольного треугольника CLA ∠CAL=90°-∠LCA ⇒ ∠ACK=∠CAL.
Поэтому треугольники ACK и CAL равны по общей стороне AC и прилежащим углам, откуда KC=AL.
Кроме того, из равенства тех же углов следует, что треугольник ABC равнобедренный, AB=CB.
Далее, по условию AL=BK, а поскольку мы доказали, что AL=KC, можно сделать вывод, что BK=KC, то есть высота AK одновременно является медианой. Отсюда следует, что AB=AC (ведь треугольники AKB и AKC оказываются равными по двум сторонам и углу между ними).
Вывод: AB=BC=AC, то есть треугольник ABC равносторонний.