Предмет: Алгебра,
автор: uwwuq
знайти точку максимуму функцій
Приложения:
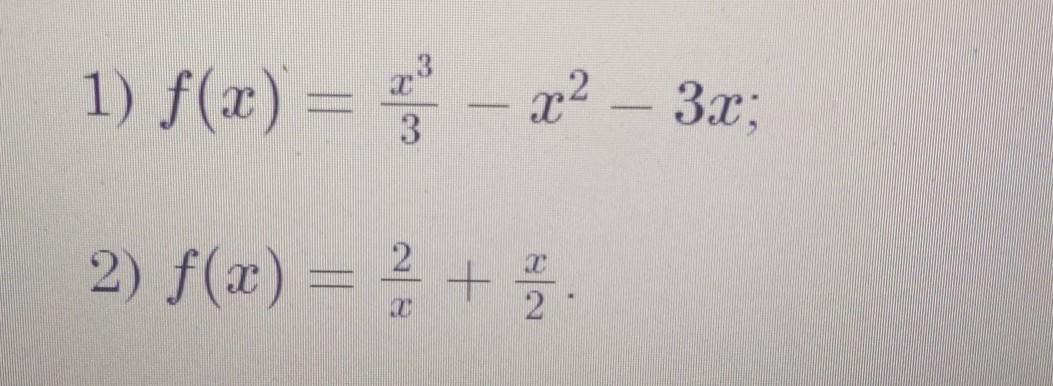
Ответы
Автор ответа:
1
Пояснення:
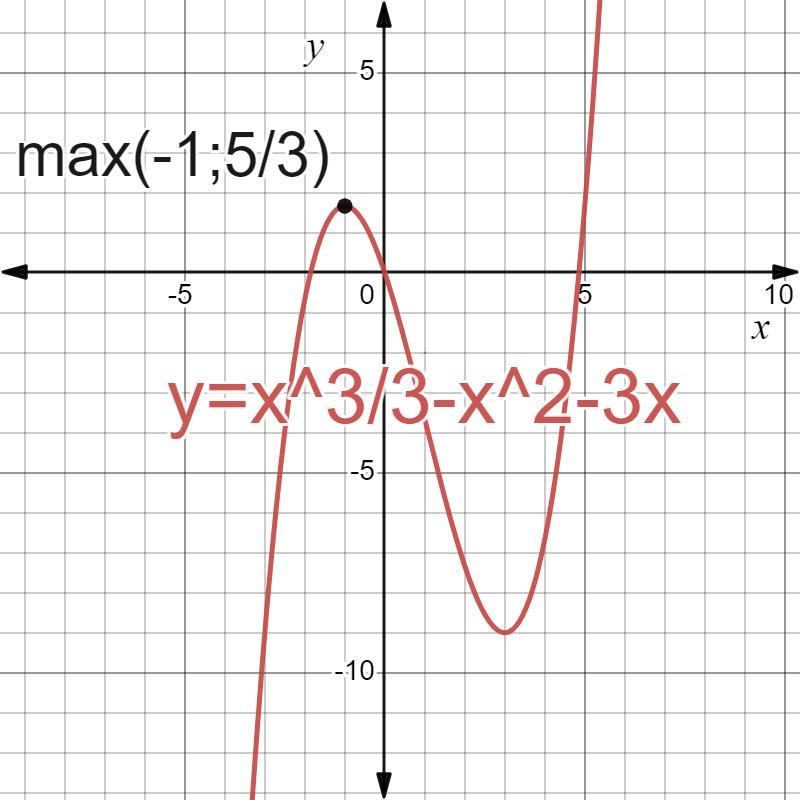
1)
Знайдемо другу похідну:
Відповідь: f(-1) - точка максимуму функції .
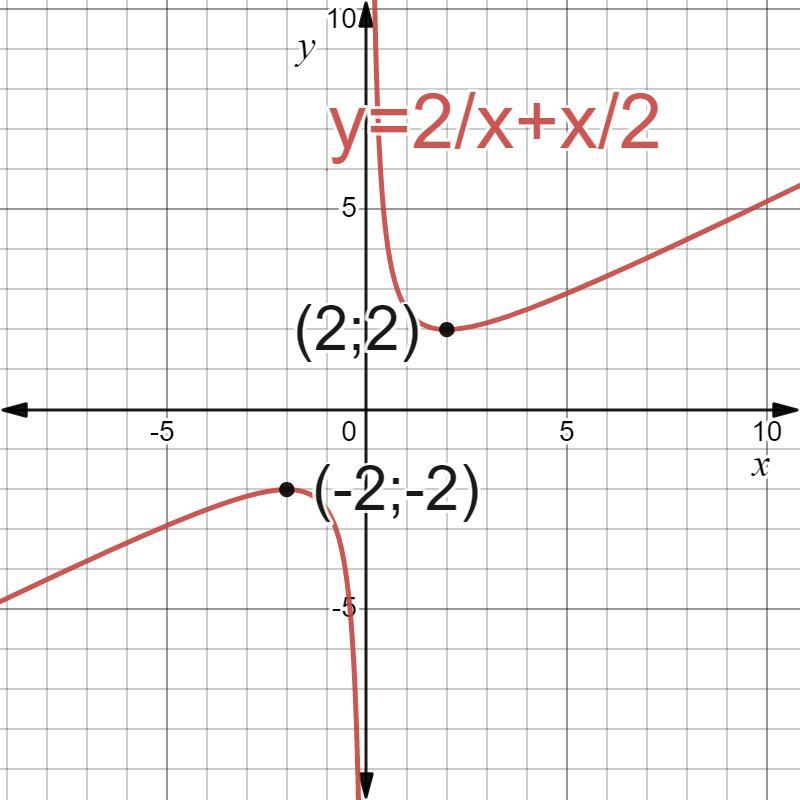
2)
Знайдемо другу похідну:
Відповідь: f(-2) - точка максимуму функції .
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: efelen1990
Предмет: Химия,
автор: abracadabra001
Предмет: Английский язык,
автор: uturova17
Предмет: Математика,
автор: grenplayer1337
Предмет: Математика,
автор: nikbystrov06