Question

Знайти площу трапеції, основи якої дорівнюють 8 см і 14 см, а діагональ довжиною 12 см
утворює з більшою основою кут 30°.

Answer 1

Ответ:

Пошаговое объяснение:Для знаходження площі трапеції можемо скористатись формулою:

Площа трапеції = (сума основ * висота) / 2

Знаємо, що одна основа дорівнює 8 см, інша - 14 см, а діагональ - 12 см. Крім того, знаємо, що кут між діагоналлю і більшою основою дорівнює 30°.

Щоб знайти висоту, можемо скористатись тригонометричними співвідношеннями:

висота = діагональ * sin(кут)

висота = 12 см * sin(30°)

висота ≈ 6 см

Тепер, можемо знайти площу:

Площа трапеції = (8 см + 14 см) * 6 см / 2

Площа трапеції = 22 см * 6 см / 2

Площа трапеції = 66 см²

Отже, площа трапеції дорівнює 66 квадратних сантиметрів.

Answer 2

Відповідь: 66 см²

Покрокове пояснення:

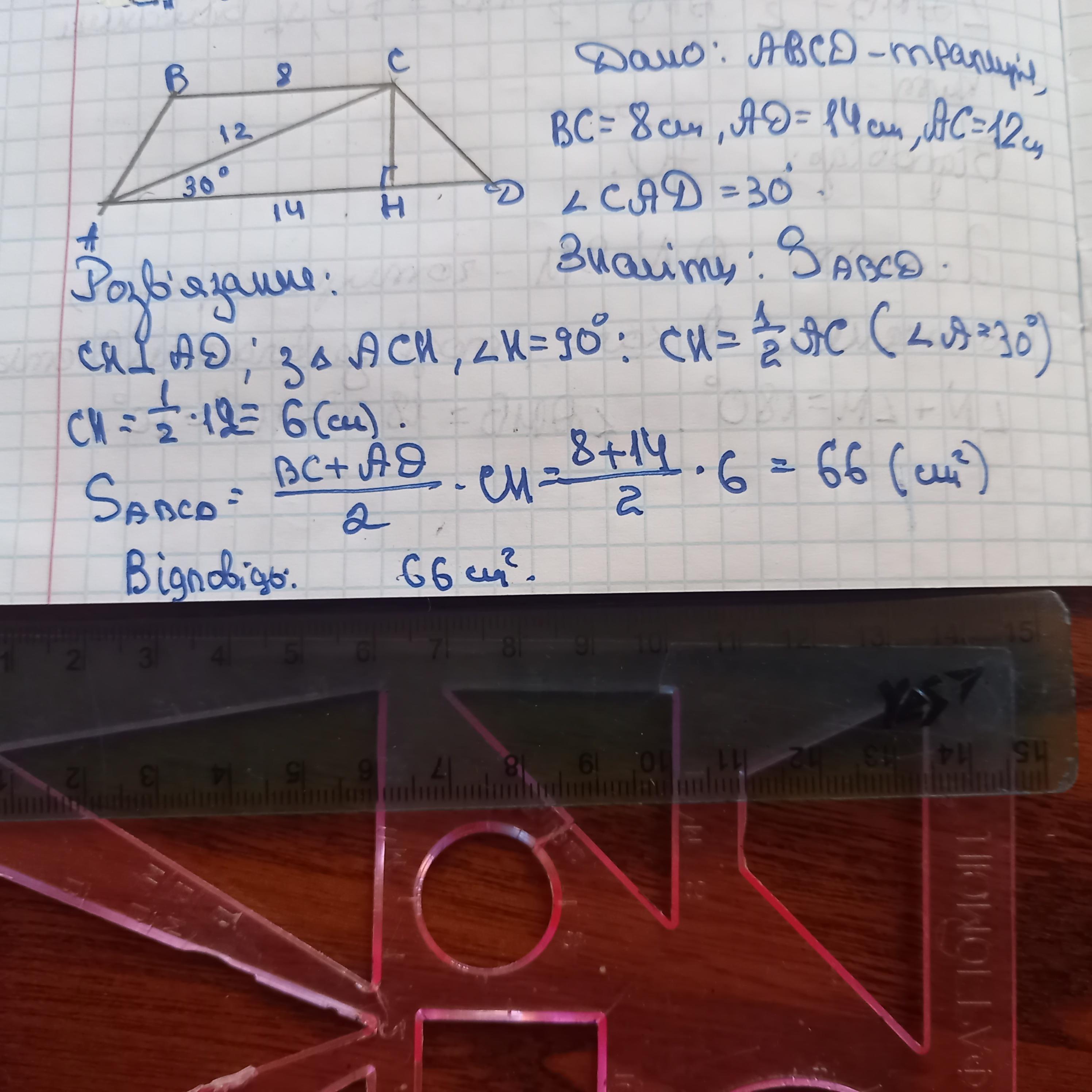
розв'язання завдання додаю