Question

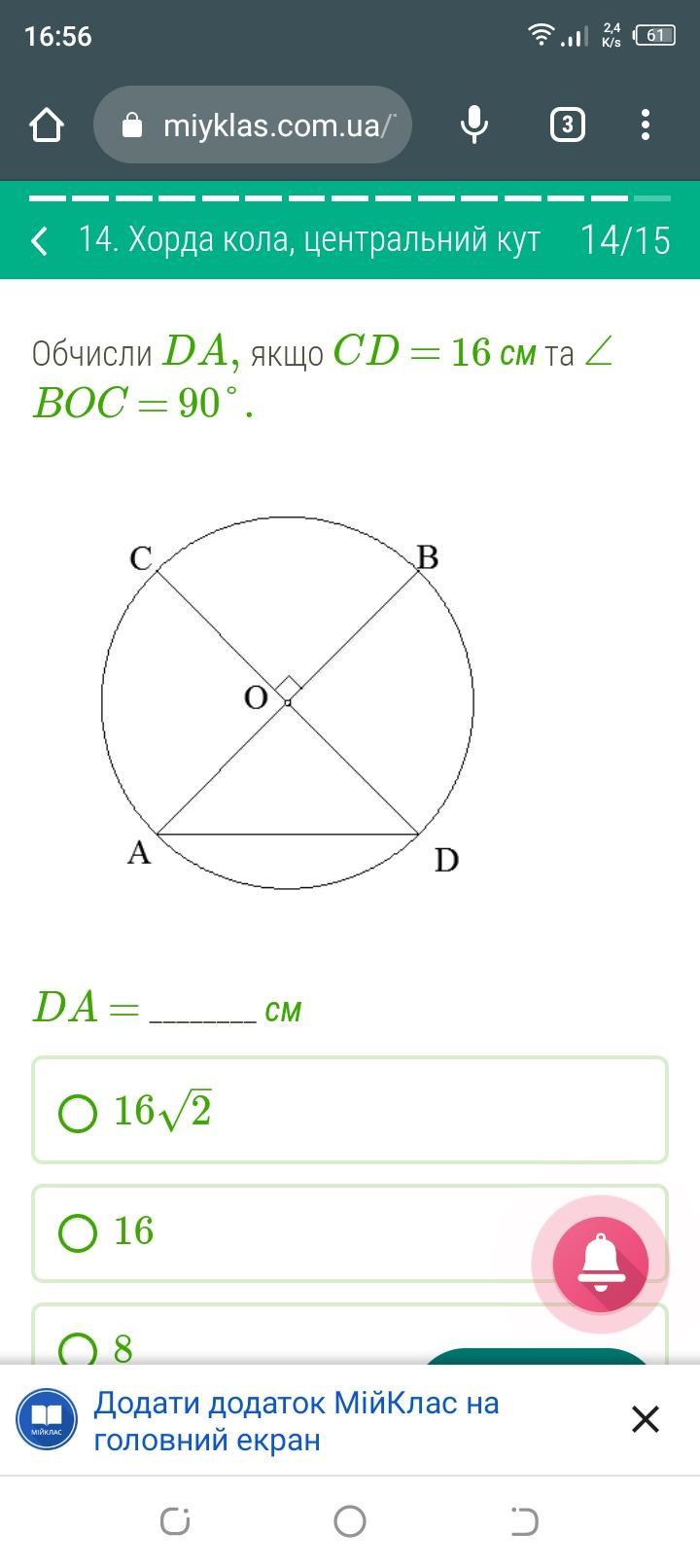
Обчисли DA, якщо CD = 16 см та ∠ BOC = 90°.

Answer 1

Відповідь:

Будемо використовувати теорему Піфагора для трикутника ACD:

AC^2 = AD^2 + CD^2

Також з умови маємо, що ∠BOC = 90°, тому BC - діаметр кола описаного навколо чотирикутника ABCD, а отже, ∠BAC = ∠BDC = 90°/2 = 45°.

Таким чином, маємо наступну систему рівнянь:

AC^2 = AD^2 + CD^2

AD + DC = AC

CD = 16 см

∠BAC = ∠BDC = 45°

Застосуємо теорему косинусів до трикутника ACD, щоб знайти AD:

AC^2 = AD^2 + CD^2 - 2AD·CD·cos(∠ACD)

Оскільки ∠ACD = ∠BAC + ∠BDC = 45° + 45° = 90°, то cos(∠ACD) = 0, тому рівняння спрощується до:

AC^2 = AD^2 + CD^2

Підставляємо відомі значення і розв'язуємо для AD:

AC^2 - CD^2 = AD^2

(2BC)^2 - CD^2 = AD^2

(2·6)^2 - 16^2 = AD^2

36 - 256 = AD^2

AD^2 = -220 (від'ємне значення - неможливо)

Отже, такого трикутника не існує.

Пояснення: