100 БАЛЛОВ!
Задание 1.
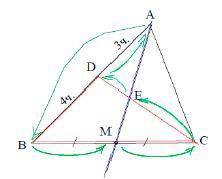
Задан треугольник ABC, из вершины A которого проведена медиана AM. На стороне AB отметили точку D так, что AD : DB = 3 : 4. В каком отношении медиана AM делит отрезок CD? Решите задачу, используя теорему Менелая.
Задание 2
Задан треугольник ABC, на сторонах AB и BC которого отмечены точки C1 и A1 соответственно. Из точки B проведена медиана BB1. Отрезки AA1, BB1 и CC1 пересекаются в точке O. Используя теорему Чевы, докажите, что A1C1 || AC.
Задание 3.
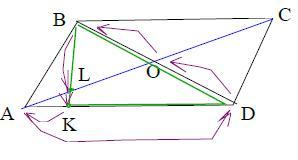
Задан параллелограмм ABCD, диагонали которого пересекаются в точке O. На стороне AD отметили точку K так, что AK = 1/5 AD. На диагонали AC отметили точку L так, что AL = 1/6 AC. Используя теорему Менелая, докажите, что точки B, L и K лежат на одной прямой.
Ответы
Ответ:
Объяснение:
Задание 1.
Дано:
ΔАВС
АМ - медиана
AD : DB = 3 : 4
-----------------------
DE : EC = ?
Рассмотрим ΔВDС с секущей AM.
По теореме Менелая (запись ведем по стрелкам):
(BM/MC) * (CE/ED) * (DA/AB) = 1.
ВМ = МС, т.к. АМ - медиана → BM/MC = 1. Тогда
(CE/ED) * (DA/AB) = 1
BD = 4ч., DA = 3ч. по условию. Тогда
AB = BD + DA = 4 + 3 = 7 (ч.)
Получаем:
(CE/ED) *(3/7) = 1
СE : ED = 1 : (3/7)
СE : ED = 7 : 3 или
ED : CE = 3 : 7
Задание 2.
Дано:
ΔАВС
т. С₁ ∈ АВ
т. А₁ ∈ ВС
ВВ₁ - медиана
т. О - точка пересечения ВВ₁, АА₁, СС₁
Док., A₁C₁ || AC
Теорема Чевы: любые произвольные отрезки, выходящие из вершин Δ-ка, (но с одним условием: они должны пересекаться в одной точке) делят противолежащие этим вершинам стороны таким образом, что истинно равенство:
(АС₁/С₁В) * (ВА₁/А₁С) * (СВ₁/В₁А ) = 1.
т.к. ВВ₁ - медиана, то СВ₁ = В₁А и СВ₁/В₁А = 1. Тогда
(АС₁/С₁В) * (ВА₁/А₁С) =1, откуда
АС₁ /СВ₁ = А₁С/ВА₁, т.е. эти отрезки пропорциональны.
Можно записать так:
ВС₁/С₁А = ВА₁/А₁С
т. Фалеса (для пересекающихся секущих):
Если прямые (A₁C₁ и AC) пересекают две другие прямые (параллельные или нет) (АВ и ВС) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.
Т.е. A₁C₁ || AC, ч.т.д.
Задание 3.
Дано:
ABCD - параллелограмм
т. К ∈ AD
AK = 1/5 AD
т. L ∈ AC
AL = 1/6 AC
Док., т. В, т. L, т. K ∈ одной прямой
1) Теорема Менелая 1:
если на сторонах AB и BC треугольника ABC взяты соответственно точки C1 и A1, а точка B1 взята на продолжении стороны AC за точку C, то точки C1, A1 и B1 лежат на одной прямой тогда и только тогда, когда выполнено равенство:
(АС₁/С₁В) * (ВА₁/А₁С) * (СВ₁/В₁А ) = 1.
2) Рассмотрим ΔBKD
По т. Менела,чтобы точки лежали на одной прямой, должно быть: (пишем по стрелкам):
(DO/OB) * (BL/LK) * (AK/AD) = 1
DO = OB, т.к. диагонали параллелограмма в точке пересечения делятся пополам.
(BL/LK) * (AK/AD) = 1
AK = 1/5 AD по условию, т.е. AK/AD = 1/5
(BL/LK)* (1/5) = 1 (1)
3) Рассмотрим ΔALK и ALK ~BLC. Они подобны:
ALK ~ BLC по двум углам: ∠ALK =∠BLC как вертикальные,
∠LAK = ∠BCL как накрест лежащие при параллельных прямых AD и ВС.
Т.к. Δ-ки подобны, то
AL/LC = KL/BL, но
AL = 1/6 AC или AL/АС = 1/6. Тогда
LC = 6 - 1 =5(ч.) Получаем:
AL/LC =1/5 = KL/BL или
BL/LK = 5/1
4) Подставляем в уравнение (1):
(5/1) * (1/5) = 1
1 = 1, ч.т.д.
Т.е. точки B, L, K лежат на одной прямой ВК.