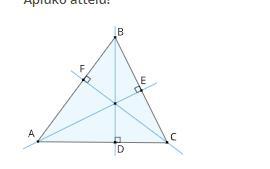
Известно, что AC=17 см, AE=14 см, CF=9 см, BD=8 см.
Вычислите площадь треугольника ABC!
S(АВС)= см2
Ответы
воспользуемся формулой Герона для вычисления площади треугольника через длины его сторон:
S = квадратный корень(p(p-a)(p-b)(p-c))
где a, b, c - длины сторон треугольника, а p - полупериметр, равный половине суммы длин сторон:
p = (a + b + c) / 2
Для треугольника ABC нужно найти длины его сторон. Обозначим точку пересечения диагоналей BD и AC как точку M. Поскольку BM делит диагональ AC пополам, то AM = MC = AC / 2 = 8,5 см.
Также заметим, что треугольники AEB и CFD подобны треугольнику ABC, поскольку углы при вершинах B и D являются соответственными. Из этого следует, что соотношение длин сторон треугольников AEB и CFD равно соотношению их высот, опущенных на сторону BC:
AE / CF = AB / CD
14 / 9 = AB / 8
AB = 112 / 9 см
Теперь мы знаем длины всех сторон треугольника ABC:
AB = 112 / 9 см, AC = 17 см, BC = 2AM = 17 см.
Полупериметр треугольника:
p = (AB + AC + BC) / 2 = (112/9 + 17 + 17) / 2 = 89/3 см.
Площадь треугольника:
S = квадратный корень (p(p-a)(p-b)(p-c)) = квадратный корень(89/3 * (89/3 - 112/9) * (89/3 - 17) * (89/3 - 17)) ≈ 84,7 (кв. см).
Ответ: S(ABC) ≈ 84,7 кв. см.