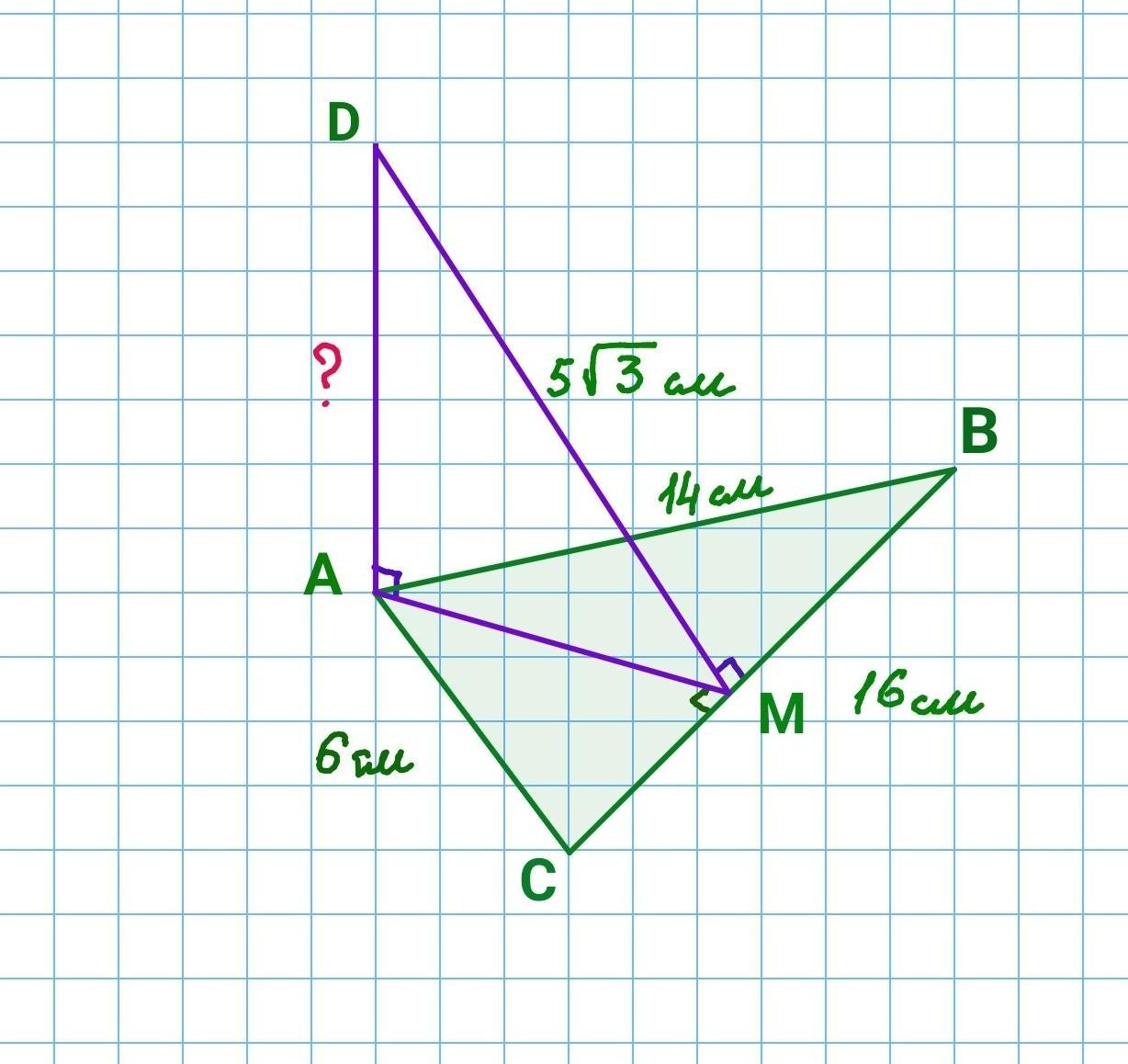
ПРОШУ НЕ БРАТИ ЧУЖУ ВІДПОВІДЬ! Сторони трикутника дорівнюють 14 см. 16 см і 6 см. Із вершини більшого кута трикутника до його площини проведено перпендикуляр. Відстань від верхнього кінця перпендикуляра до більшої сторони дорівнює 5корінь3 см. Знайдіть довжину цього перпендикуляра
Ответы
Ответ:
Довжина перпендикуляра дорівнює 4√3 (см)
Объяснение:
Сторони трикутника дорівнюють 14 см. 16 см і 6 см. Із вершини більшого кута трикутника до його площини проведено перпендикуляр. Відстань від верхнього кінця перпендикуляра до більшої сторони дорівнює 5корінь3 см. Знайдіть довжину цього перпендикуляра.
Нехай АВС - даний трикутник. АВ=14 см, ВС= 16 см, АС= 6 см. Так як проти більшої сторони трикутника лежить більший кут, то AD⟂(ABC), тому AD перпендикулярна до кожної прямої, що належить площині ABC.
Відстань від точки D до сторони BC трикутника - перпендикуляр, опущений з точки D на пряму BC: DM⟂BC.
Так як AD⟂(ABC), то DM - похила, а відрізок AM - проекція похилої на площину ABC.
DM⟂BC, за теоремою "про три перпендикуляри ": AM⟂BC.
⇒ AM - висота △ABC, проведена до сторони BC.
Розглянемо △ABC.
1) Знайдемо його площу за формулою Герона.
де
(см) - півпериметр △ABC.
(см²)
2) Площу трикутника ABC можна також знайти за формулою:
де а - сторона, - висота, проведена до сторони а.
Висота АМ буде дорівнювати:
(см)
3) За теоремою Піфагора знайдемо катет АD з прямокутного трикутника ADM(∠DAM=90°)
AD²=DM²-AM²=(5√3)²-(3√3)²=75-27=48
AD= 4√3 (см)
Відповідь: 4√3 см