Question

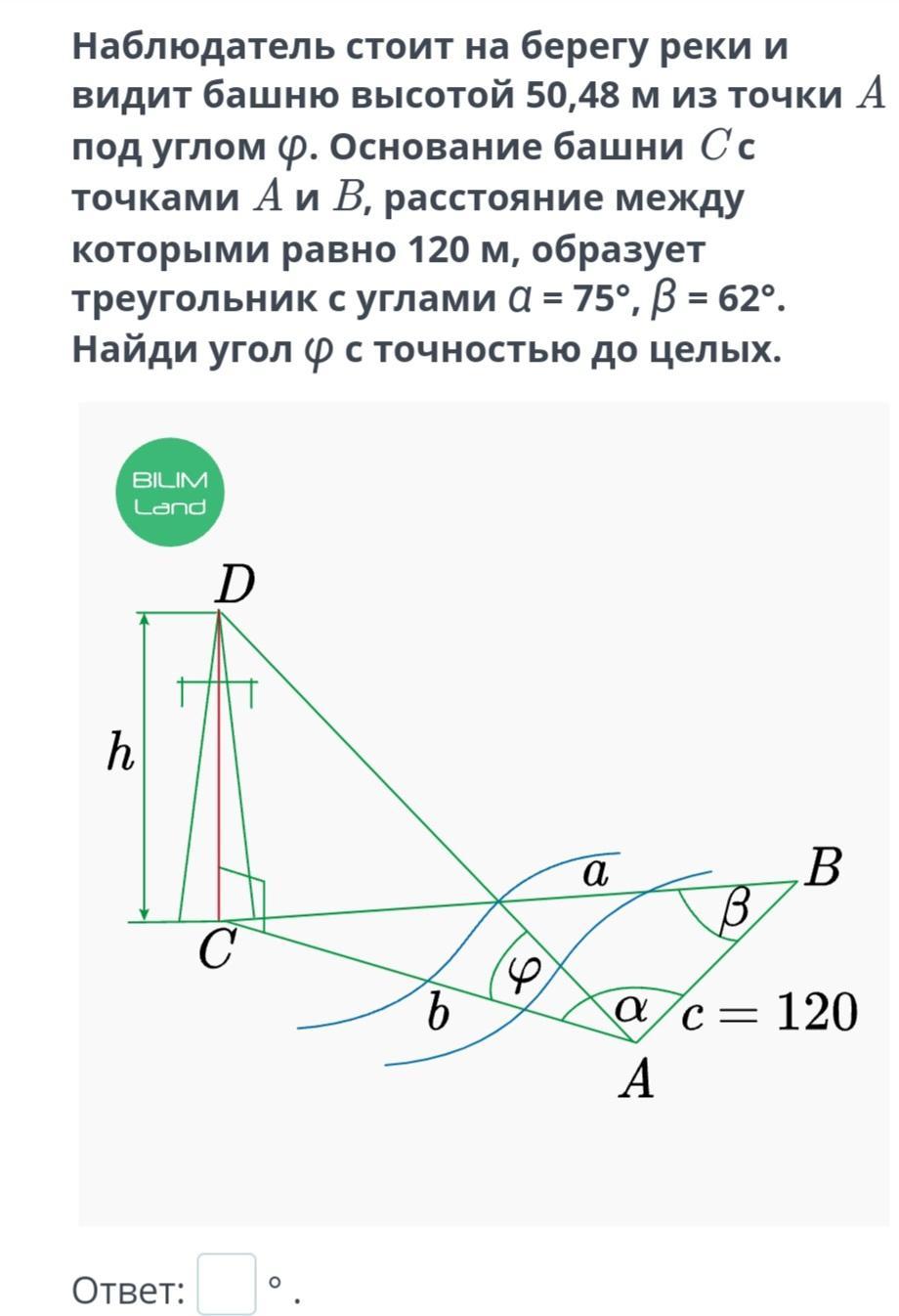
Наблюдатель стоит на берегу реки и видит башню высотой 50,48 м из точки А подуглом Ф. Основание башни Сс точками А и В, расстояние между которыми равно 120 м, образует треугольник с углами а = 75°, В = 62°. Найди угол () с точностью до целых. Помогите!

Answer 1

Ответ:

Рассмотрим треуг-к АВС .

По теореме синусов имеем     $\bf \dfrac{AB}{sinC}=\dfrac{AC}{sin\beta }$   .

$\bf \angle {C}=180^\circ -75^\circ -62^\circ =43^\circ \\\\AC=\dfrac{AB\cdot sin\beta }{sinC}=\dfrac{120\cdot sin62^\circ }{sin43^\circ }\approx \dfrac{120\cdot 0,8829}{0,6820}\approx 155,35$  

Рассмотрим треуг-к ACD .

$\bf tg\varphi =\dfrac{DC}{AC}=\dfrac{50,48}{155,35}\approx 0,3249\ \ \Rightarrow \ \ \ \varphi=arctg\, 0,3249=18^\circ$