Предмет: Алгебра,
автор: inkognitous
Упростите данное выражение, пожалуйста подробно
Приложения:
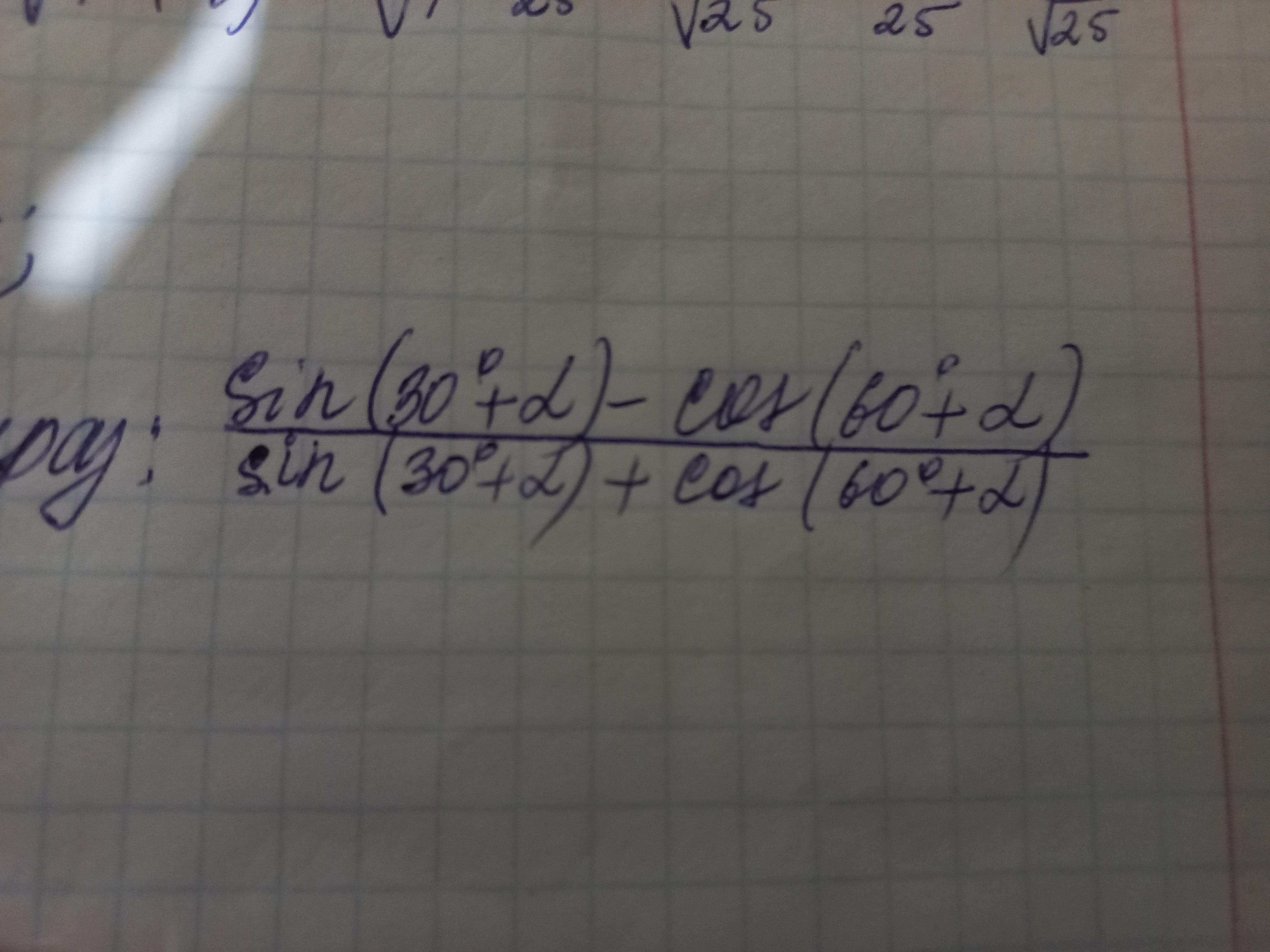
master32wsp:
уже сделал
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Другие предметы,
автор: majorovamaria041
Предмет: Русский язык,
автор: qurbanovanaida1122
Предмет: Українська література,
автор: domo19722018
Предмет: Химия,
автор: nasralbeck2
Предмет: Другие предметы,
автор: samsjf608