Question

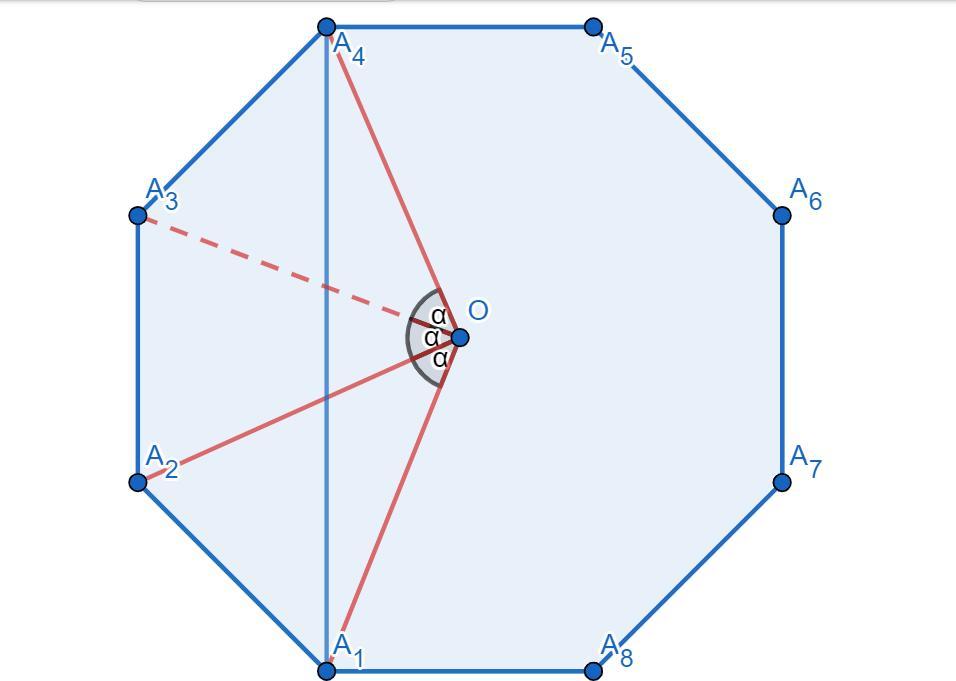
Точка O – центр правильного восьмикутника A1A2 ... A8. Доведіть, що
площі трикутників A1OA2 і A1OA4 рівні.

Answer 1

Ответ: Доведено, що площі трикутників A1OA2 і A1OA4 рівні.

Объяснение:

*Центральный угол n-го угольника вычисляется по формуле :

$\boldsymbol{\alpha = \dfrac{360^{\circ}}{n} }$  

**Площадь треугольника  по двум сторонам и углу между ними вычисляется формулой :

$\boldsymbol{S _{\triangle }= \dfrac{1}{2}\cdot a\cdot b \cdot \sin \alpha }$

Поскольку ∠A₁OA₂   центральный угол правильного восьмиугольника , то

$\alpha = \angle A_1 O A_2 =\dfrac{360}{8} = 45^{\circ}$

За счет того что наш восьмиугольник правильный ,  отрезки проведенные из центра восьмиугольника к его вершинам равны

Поэтому :

A₁O = A₂O = A₄O = x

Теперь мы можем довольно просто найти площадь ΔA₁OA₂ , зная величины двух сторон и угол между ними :

$S_{A_1OA_2 } =\dfrac{1}{2} \cdot A_2O \cdot A_1O \cdot \sin \alpha =\dfrac{1}{2}\cdot x \cdot x \cdot \sin 45^{\circ} = \boxed{\dfrac{x^2\sqrt{2} }{4}}$

Рассматривая ΔA₁OA₄  можно легко заметить , что ∠A₁OA₄ состоит из трех центральных углов ⇒  ∠A₁OA₄ = 3·45 = 135°

По двум сторонам  A₄O = A₁O = x и  углу ∠A₁OA₄ = 135°   находим площадь  ΔA₁OA₄

$S_{A_1OA_4} =\dfrac{1}{2} \cdot x\cdot x \cdot \sin 135^{\circ} =\boxed{ \dfrac{x^2 \sqrt{2} }{4}}$

Сравнив получившиеся  площади , мы получили что площадь ΔA₁OA₂  равна ΔA₁OA₄

#SPJ1