Предмет: Геометрия,
автор: Аноним
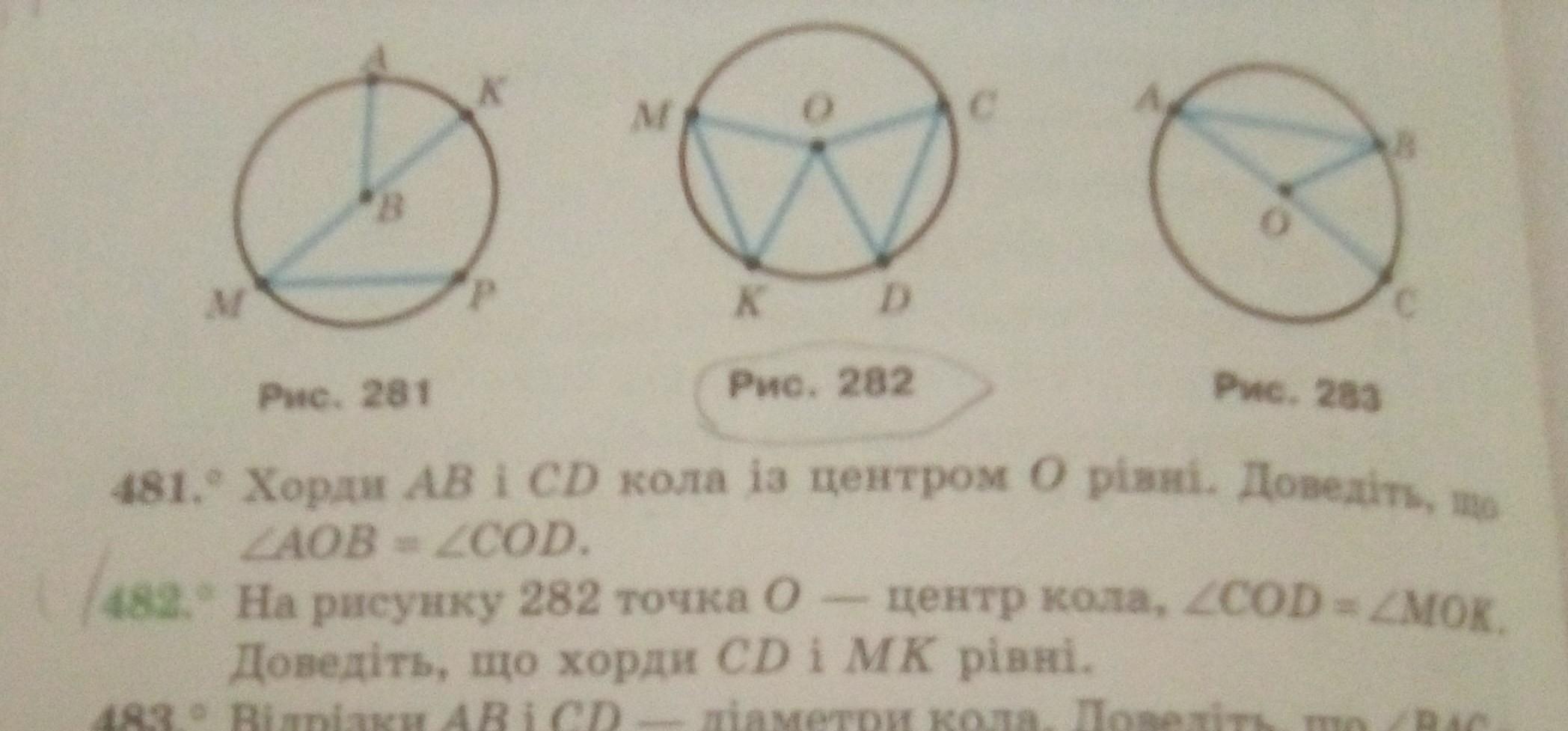
На рисунку 282 точка О центр кола, кут COD=куту MOK. Доведіть, що хорди СD i МК рiвнi.
Допоможіть дам 100 балів.
лише номер 482.
Приложения:
Ответы
Автор ответа:
9
Відповідь:
Перш за все, оскільи точка O є центром кола, то відрізок ОС дорівнює відрізку ОД. Також, оскільки точка O є центром кола, то відрізок ОМ дорівнює відрізку ОК.
Далі, оскільки кут COD дорівнює куту MOK, то трикутники СОD і КОМ є подібними за спільним кутом і стороною. З цього випливає, що співвідношення довжин сторін в цих трикутниках дорівнює співвідношенню довжин їх відповідних сторін:
CD / OM = OD / OK
Оскільки ОД дорівнює ОС і ОК дорівнює ОМ, то ми можемо переписати це співвідношення як:
CD / OM = OC / OM
Звідси випливає, що CD дорівнює MK. Тому хорди CD і МК рівні, як і потрібно було довести.
Пояснення:
Похожие вопросы
Предмет: Немецкий язык,
автор: vika716671
Предмет: Алгебра,
автор: semyons26
Предмет: История,
автор: SeverysSnape1
Предмет: Русский язык,
автор: egoreeonegue
Предмет: Математика,
автор: fariza1357