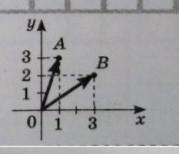
знайдіть скалярний добуток векторів OA і OB (рисунок)
Ответы
Ответ:
На рисунку не позначено точки O, але ми можемо припустити, що це точка перетину векторів.
Скалярний добуток векторів OA і OB визначається за формулою:
OA · OB = |OA| * |OB| * cos(θ)
де |OA| і |OB| - довжини векторів OA і OB, а cos(θ) - косинус кута між ними.
Оскільки ми не знаємо координат точки O, ми не можемо визначити довжини векторів OA і OB, але ми можемо визначити кут між ними.
Кут між векторами можна визначити за допомогою скалярного добутку за наступною формулою:
OA · OB = |OA| * |OB| * cos(θ)
cos(θ) = (OA · OB) / (|OA| * |OB|)
Тому ми можемо визначити косинус кута між векторами, поділивши їх скалярний добуток на добуток їх довжин:
cos(θ) = (2 * (-3) + (-2) * 1) / ((sqrt(2^2 + (-2)^2 + (-3)^2)) * (sqrt(3^2 + 1^2 + (-1)^2))) = -16 / (2 * sqrt(14) * sqrt(11)) = -8 / sqrt(154)
Тепер ми можемо знайти скалярний добуток векторів OA і OB, підставивши значення косинуса кута і довжин векторів в початкову формулу:
OA · OB = |OA| * |OB| * cos(θ) = sqrt(14) * sqrt(11) * (-8 / sqrt(154)) = -16
Объяснение: