Предмет: Математика,
автор: zxcking123
!!СРОЧНО!!!
Розв'язати систему рівнянь повністю
Приложения:
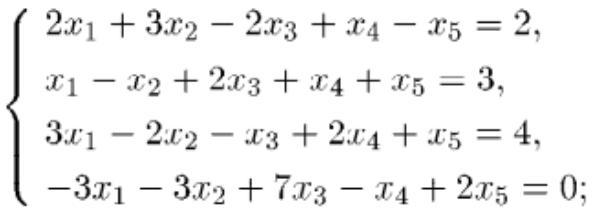
Ответы
Автор ответа:
1
Ответ:
Решаем систему неравенств методом Гаусса.
Выпишем матрицу системы вместе с расширенной матрицей и преобразуем их с помощью элементарных преобразований к ступенчатому виду .
1 строку умножим на (-2) и сложим со 2 строкой,
1 стр. * (-3) + 3стр. ; 1 стр. * 3+ 4 стр. Затем поменяем 2 стр. и 3 стр.
2 стр. * (-6) + 3 стр. ; 3 стр. + 4 стр.
3 cтр. * (-7) + 4 стр. * 36
Ранг матрицы системы равен рангу расширенной матрицы , r=4 . Значит система совместна . Количество неизвестных равно n=5 . Значит система имеет бесчисленное множество решений и свободное неизвестное одно (5-4=1) . Выбираем в качестве свободного неизвестного х₅ .
Запишем систему на основании последней ступенчатой матрицы :
Ответ:
Похожие вопросы
Предмет: География,
автор: yaremenkokostya10
Предмет: Алгебра,
автор: 29Danil29
Предмет: Математика,
автор: nPiBeTkIt
Предмет: Алгебра,
автор: hasos76663