решите ....................
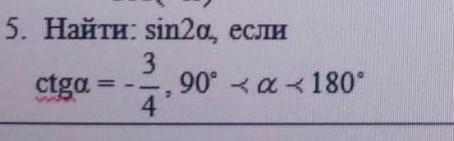
Ответы
Ответ.
Найти .
Тождество :
Применяем формулу .
Замечание. Докажем формулу.
Ответ:
Решение:
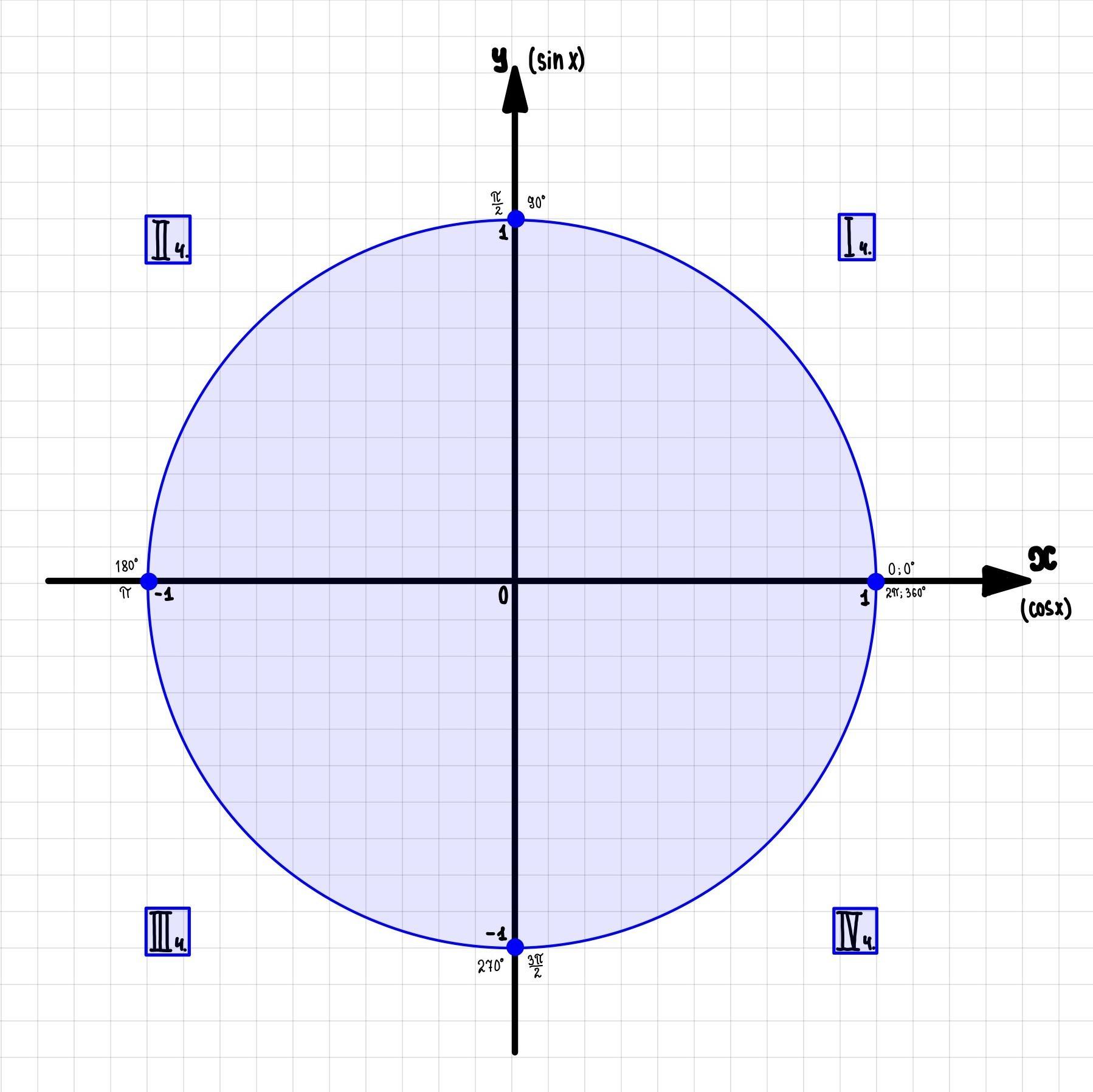
→ Сначала нам нужно определить - в какой четверти находится угол α. Для этого обратимся к тригонометрической единичной окружности (см. вложение).
Мы видим, что находится между двумя точками:
и
. Следовательно угол
находится во II четверти. Отсюда следует, что:
Теперь можем приступить к вычислениям.
→ Нам известно, что . Зная котангенс угла мы можем найти синус этого же угла. Для этого воспользуемся одним из следствий основного тригонометрического тождества:
(Данную формулу мы можем получить, поделив обе части основного тригонометрического тождества на :
).
Следовательно:
Значит:
±
±
±
.
Мы получаем, что равен или
, или
. Исходя из условия
, значит нам подходит вариант:
.
→ Зная синус угла мы можем найти косинус того же угла, воспользовавшись формулой основного тригонометрического тождества:
Следовательно:
Значит:
±
±
±
И снова мы получаем, что равен или
, или
. Обратившись к условию, вспоминаем, что
, значит нам подходит вариант:
.
→ И нам осталось найти . Воспользуемся формулой синуса двойного угла:
(!) Данную формулу мы можем вывести из более общей формулы синуса суммы двух углов:
Тогда нужно представить синус двойного угла, как синус суммы двух одинаковых углов:
Значит:
__________
Удачи Вам! :)