Предмет: Геометрия,
автор: mashapopsik
в прямоугольнике трапеции авср большая боковая сторона равна 2√7см, р равен 45°, а высота сн делит основание ар пополам. найдите площадь трапеции
даю 50 баллов
Ответы
Автор ответа:
1
В прямоугольной трапеции АВСР большая боковая сторона равна 2√7 см, ∠Р= 45°, а высота СН делит основание АР пополам. Найдите площадь трапеции.
Ответ:
21 см²
Объяснение:
Дано: АВСР - трапеция, СР=2√7 см, ∠Р=45°, АН=РН. S(АВСР) - ?
ΔСРН - прямоугольный, ∠НСР=90-45=45°, значит СН=РН.
Пусть СН=РН=х см, тогда по теореме Пифагора
СР²=х²+х²; 2х²=28; х²=14; х=√14.
СН=РН=АН=ВС=√14 см.
Площадь трапеции равна полусумме оснований умноженной на высоту.
S=(ВС+АР)/2 * СН=(√14+2√14)/2 *√14=(3√14)/2*√14=21 см²
Приложения:
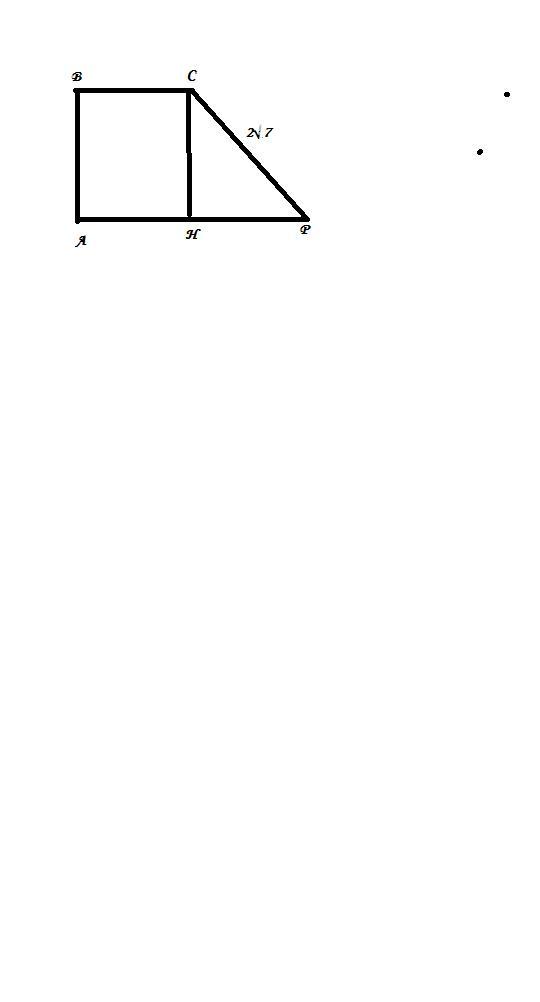
Похожие вопросы
Предмет: Українська мова,
автор: androedmuxa2023
Предмет: Геометрия,
автор: FlastMix
Предмет: Английский язык,
автор: lerachernenko2011
Предмет: Қазақ тiлi,
автор: birganymberikkizi55
Предмет: Математика,
автор: anntereshonokchai