Предмет: Алгебра,
автор: BlackFox2030
Помогите с алгеброй.
Нужно найти производную по формуле:
(U×V)¹=U¹×V+U×V¹
Приложения:
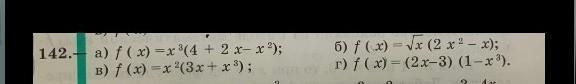
Ответы
Автор ответа:
3
а) u=x³; v=(4+2x-x²)
f'=3x²*(4+2x-x²)+(2-2x)*x³=12x²+6x³-3x⁴+2x³-2x⁴=-5x⁴+8x³+12x²
б) f'=(1/(2√x))(2x²-x)+√x*(4x-1)=(2x²-x+8x²-2x)/(2√x)=(10x²-3x)/(2√x)
в) f'=2x*(3x+x³)+x²*(3+3x²)=6x²+2x⁴+3x²+3x⁴=9x²+5x⁴
г) f'=2*(1-x³)+(2x-3)*(-3x²)=2-2x³-6x³+9x²=-8x³+9x²+2
(xⁿ)'=n*xⁿ⁻¹
BlackFox2030:
как мы получили 8х²? (в 142 номере пример г)
привели к общему знаменателю 2√x
Похожие вопросы
Предмет: Химия,
автор: prokopecdima7
Предмет: Українська література,
автор: dimamakortet054
Предмет: Алгебра,
автор: smartshop182023
Предмет: Русский язык,
автор: boomwolfg