Предмет: Геометрия,
автор: rc0922f
ПОМОГИТЕ, ДАЮ 30 БАЛЛОВ!!!
С рисунком и условием, пожалуйста)
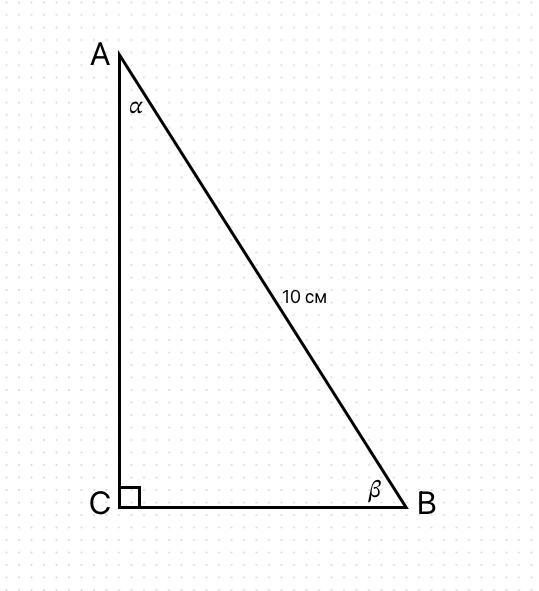
1) У прямокутному трикутнику гіпотенуза дорівнює 10 см, а синус одного з гострих кутів - 8/10. Знайдіть катети трикутника.
Ответы
Автор ответа:
3
Відповідь:
6см та 8см
Пояснення:
Нехай наш трикутник ABC.
В ньому ∠С = 90°. Позначимо кути А як , а B як
Що таке синус кута?
Синус гострого кута прямокутного трикутника - це відношення протилежного катета до гіпотенузи
Тобто
,
В умові сказано, що синус одного з гострих кутів =
Припустимо, що саме відомий синус одного з гострих кутів - це sin , тоді
З іншої сторони
Отже
см
За теоремою Піфагора знайдемо AC
см
Якщо ж , то
AC = 8 см
За теоремою Піфагора знайдемо BC
см
Приложения:
Похожие вопросы
Предмет: Литература,
автор: offfner1
Предмет: География,
автор: 2008dovlyatova
Предмет: Биология,
автор: etoile72
Предмет: Физика,
автор: aanakanybekovna
Предмет: Алгебра,
автор: levcukroman03