Предмет: Геометрия,
автор: arkins723
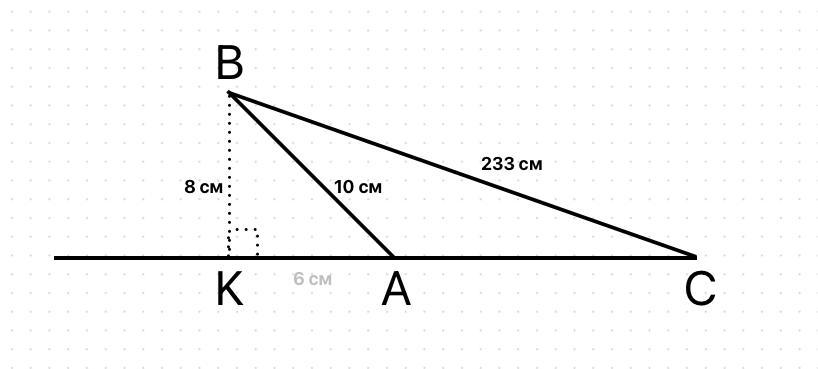
У трикутнику АВС ﮮА—тупий , ВС= 233 ,
АВ=10см, ВК=8см—висота трикутника. Знайдіть АС.
Ответы
Автор ответа:
2
Відповідь:
226.86 см
Пояснення:
Проведемо одну з висот трикутника BK, яка буде за межами трикутника ABC.
Розглянемо трикутник ABK.
Це прямокутний трикутник в якому AB = 10cм, BK = 8см, тому за теоремою Піфагора знайдемо AK
см
Отже AK = 6 см.
Розглянемо трикутник BKC.
Це прямокутний трикутник в якому BK = 8см, BC = 233 см
За теоремою Піфагора знайдемо KC
см
Отже КС = або KC ≈ 232.86 см
З іншої сторони КС = AK + AC. Звідси
AC = KC - AK = 232.86 - 6 = 226.86 см
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: Huiputalo5
Предмет: Русский язык,
автор: elizavetaveder50
Предмет: Алгебра,
автор: zenakukik527
Предмет: Английский язык,
автор: komila04
Предмет: Математика,
автор: bazhenov8ogdans