Предмет: Геометрия,
автор: Аноним
Помогите пожалуйста 100 баллов
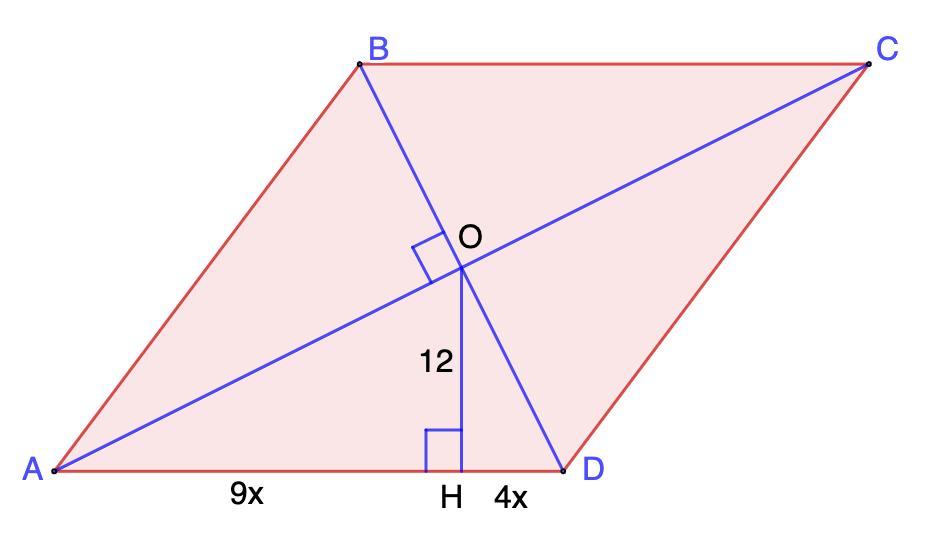
Перпендикуляр, опущенный из точки пересечения диагоналей ромба на его сторону, равен 12 и делит эту сторону на отрезки, относящиеся как 4: 9. Найдите диагонали ромба.
Приложения:

Ответы
Автор ответа:
0
Ответ:
Диагонали ромба равны 12√13 и 8√13.
Объяснение:
Перпендикуляр, опущенный из точки пересечения диагоналей ромба на его сторону, равен 12 и делит эту сторону на отрезки, относящиеся как 4: 9. Найдите диагонали ромба.
Дано: ABCD - ромб;
АС и BD - диагонали;
ОН ⊥ AD;
DH : AH = 4 : 9
Найти: АС и BD.
Решение:
Рассмотрим ΔAOD.
- Диагонали ромба взаимно перпендикулярны.
⇒ ΔAOD - прямоугольный.
ОН - высота.
- Метрические отношения в прямоугольном треугольнике:
- 1. Квадрат высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению проекций катетов на гипотенузу.
- 2. Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.
OH = 12; DH : AH = 4 : 9
Пусть DH = 4x, тогда AH = 9x.
1. OH² = DH · AH
144 = 4x · 9x
36x² = 144
x² = 4 ⇒ x = 2
DH = 8; AH = 18; AD = 18 + 8 = 26.
2. AO² = AH · AD = 18 · 26 = 468 ⇒ AO = √468 = 6√13
OD² = HD · AD = 8 · 26 = 208 ⇒ OD = √208 = 4√13
- Диагонали ромба точкой пересечения делятся пополам.
⇒ АС = 6√13 · 2 = 12√13;
BD = 4√13 · 2 = 8√13.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: a43308448
Предмет: Информатика,
автор: naswiqqq
Предмет: География,
автор: hjfndndjf
Предмет: Литература,
автор: Аноним