Предмет: Геометрия,
автор: Аноним
САМАЯ СРОЧНАЯ РАБОТА!!!!!!!!!!!!!
Прямокутник АВСЕ перегнули по діагоналі ВЕ так що площини АВЕ та
СВЕ виявилися перпендикулярними. Знайдіть відстань між точками А і С ,
якщо менша із сторін прямокутника дорівнює 6 см, а кут між його діагоналями
60 0 . (виконати 2 рисунки)
Ответы
Автор ответа:
1
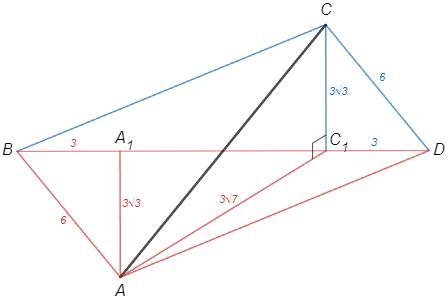
Диагонали прямоугольника равны и точкой пересечения делятся пополам. Половины диагоналей образуют равнобедренный треугольник и если угол между ними 60, то треугольник равносторонний, все углы 60.
∠ABD=60 =∠CDB
AB=6
Опустим перпендикуляры AA1 и CC1 на общую прямую BD
AA1 =AB sin60 =3√3 =CC1
BA1 =AB cos60 =3 =DC1
BD =AB/cos60 =12
A1C1 =12-3-3 =6
AC1 =√(AA1^2 +A1C1^2) =3√(3+4) =3√7
Если прямая (СС1) лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения (СС1⊥BD), то эта прямая перпендикулярна другой плоскости.
CC1⊥(ABD) => CC1⊥AC1
AC =√(CC1^2 +AC1^2) =3√(3+7) =3√10 (см)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: kairataniyaz
Предмет: Английский язык,
автор: anyaa6040
Предмет: Биология,
автор: dima109317
Предмет: Математика,
автор: dianaajmagambetova
Предмет: Биология,
автор: qwertyuioplmazh