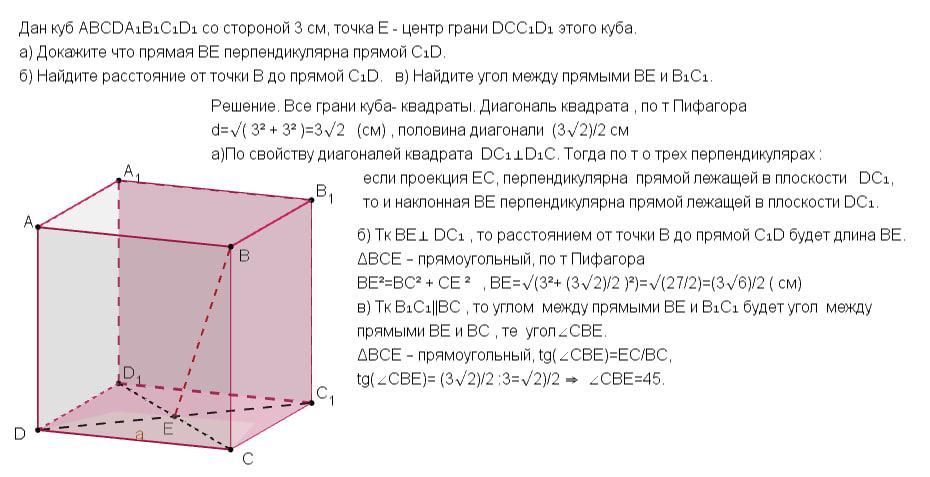
1.Дан куб ABCDA1B1C1D1 со стороной 3 см, точка Е - центр грани DCC1D1 этого куба.
а) Докажите что прямая BE перпендикулярна прямой C1D.
б) Найдите расстояние от точки B до прямой C1D.
в) Найдите угол между прямыми BE и B1C1.
Ответы
Дан куб ABCDA₁B₁C₁D₁ со стороной 3 см, точка Е - центр грани DCC₁D₁ этого куба. а) Докажите что прямая BE перпендикулярна прямой C₁D.
б) Найдите расстояние от точки B до прямой C₁D.
в) Найдите угол между прямыми BE и B₁C₁.
Решение. Все грани куба- квадраты. Диагональ квадрата , по т Пифагора
d=√( 3² + 3² )=3√2 (см) , половина диагонали (3√2)/2 см
а)По свойству диагоналей квадрата DC₁⊥D₁C. Тогда по т о трех перпендикулярах : если проекция ЕС, перпендикулярна прямой лежащей в плоскости DC₁, то и наклонная ВЕ перпендикулярна прямой лежащей в плоскости DC₁. Значит ВЕ⊥ DC₁ ВЕ⊥ DC₁.
б) Тк ВЕ⊥ DC₁ , то расстоянием от точки B до прямой C₁D будет длина ВЕ.
ΔВСЕ – прямоугольный, по т Пифагора ВЕ²=ВС² + СЕ ² ,
ВЕ=√(3²+ (3√2)/2 )²)=
=√(27/2)=(3√6)/2 ( см)
в) Тк B₁C₁||BC , то углом между прямыми BE и B₁C₁ будет угол между прямыми BE и BC , те ∠СВЕ.
ΔВСЕ – прямоугольный, tg(∠СВЕ)=ЕС/ВС,
tg(∠СВЕ)= (3√2)/2 :3=√2)/2 ⇒ ∠СВЕ=45.