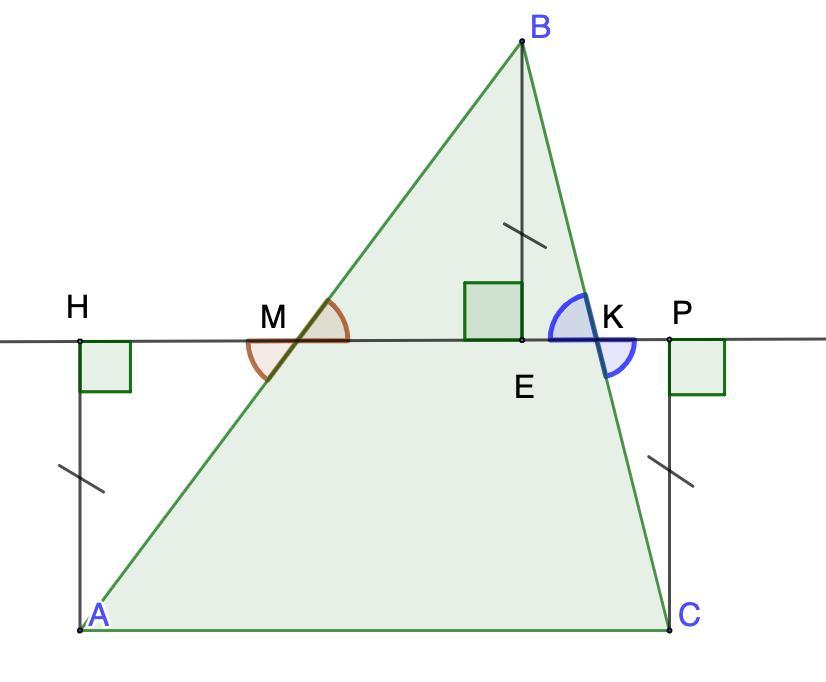
Прямая пересекает стороны АВ и ВС треугольника ABC в точках М и К соответственно. Вершины данного треугольника равноудалены от прямой МК. Докажите, что точки М и К являются серединами сторон АВ и ВС СООТВЕТСТВЕННО. прошу есть 1 час
Ответы
Ответ:
Доказано, что точки М и К являются серединами сторон АВ и ВС СООТВЕТСТВЕННО.
Объяснение:
Прямая пересекает стороны АВ и ВС треугольника ABC в точках М и К соответственно. Вершины данного треугольника равноудалены от прямой МК. Докажите, что точки М и К являются серединами сторон АВ и ВС СООТВЕТСТВЕННО.
Дано: ΔАВС;
М ∈ АВ; К ∈ ВС;
Вершины ΔАВС равноудалены от прямой МК.
Доказать: АМ = МВ; ВК = КС.
Доказательство:
- Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.
⇒ АН ⊥ МК; ВЕ ⊥ МК; СР ⊥ МК; АН = ВЕ = СР.
1. Рассмотрим ΔАНМ и ΔВЕМ - прямоугольные.
АН = ВЕ (условие)
- Вертикальные углы равны.
⇒∠НМА = ∠ВМЕ (вертикальные)
ΔАНМ = ΔВЕМ (по катету и острому углу)
- В равных треугольниках против равных углов лежат равные стороны.
⇒ АМ = МВ
2. Рассмотрим ΔСРК и ΔВЕК - прямоугольные.
СР = ВЕ (условие)
⇒∠СКР = ∠ВКЕ (вертикальные)
ΔСРК = ΔВЕК (по катету и острому углу)
⇒ СК = КВ.
АМ = МВ; СК = КВ
⇒ точки М и К являются серединами сторон АВ и ВС СООТВЕТСТВЕННО.