Предмет: Алгебра,
автор: vovavoevodin0
Розв'яжiть нерiвнiсть: x² + x - 30 < 0;
срочно
Ответы
Автор ответа:
1
Відповідь:
Можна розв'язати цю нерівність, застосовуючи методи факторизації квадратного трьохчлена та інтервального аналізу:
x² + x - 30 < 0
Спочатку знаходимо корені квадратного рівняння, що відповідає даному квадратному трьохчлену:
x² + x - 30 = 0
(x + 6)(x - 5) = 0
Отже, маємо два корені: x = -6 та x = 5.
Тепер перевіримо знаки цього квадратного трьохчлена на інтервалах, що відповідають цим кореням:
x < -6: (-)(-)(-) = -
-6 < x < 5: (+)(-)(-) = +
x > 5: (+)(+)(+) = +
Отже, розв'язком нерівність є множина значень x, для яких x належить інтервалу (-6, 5):
-6 < x < 5.
aarr04594:
Поясніть вираз : "Можна розв'язати цю нерівність, застосовуючи методи факторизації квадратного трьохчлена та інтервального аналізу:"
Автор ответа:
1
Відповідь: (-6;5)
Пояснення:
розв'язання завдання додаю
Приложения:
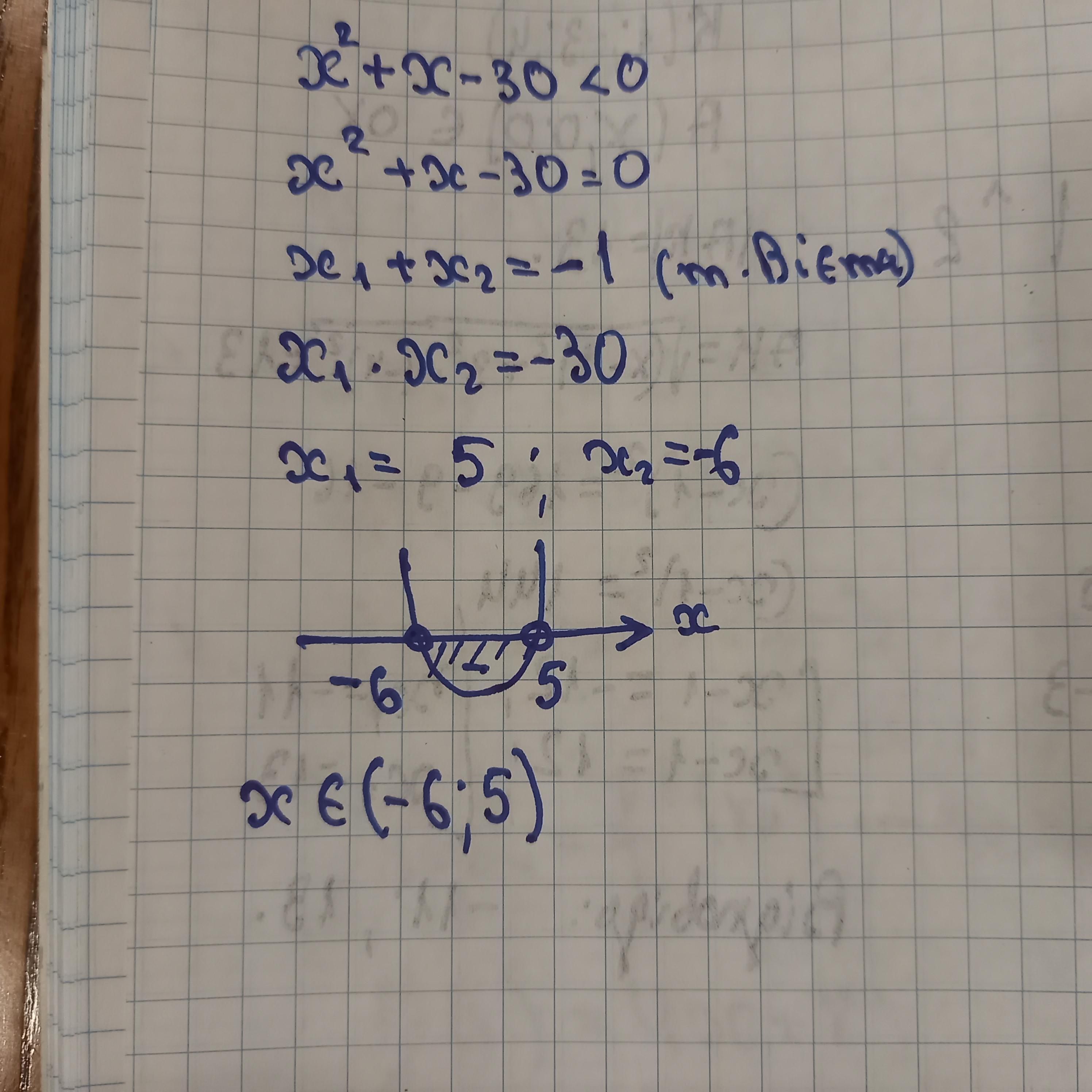
Похожие вопросы
Предмет: История,
автор: aim666992
Предмет: Қазақ тiлi,
автор: kowe4ka89
Предмет: Английский язык,
автор: kaussar0911
Предмет: Математика,
автор: oh13