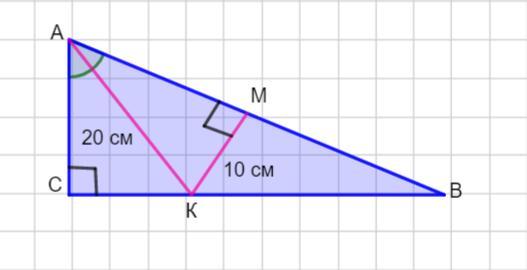
В прямоугольном треугольнике ABC угол C - прямой. Биссектриса АК равна 20 см. Расстояние от точки К до прямой AB равно 10 см. Найдите градусную меру угла АКВ.
Ответы
Ответ:
120°.
Объяснение:
В прямоугольном треугольнике АВС угол С - прямой . Биссектриса АК равна 20 см. Расстояние от точки К до прямой АВ равно 10 см. Найдите градусную меру угла АКВ.
Пусть дан ΔАВС - прямоугольный , так как ∠С =90°.
АК - биссектриса.
Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.
Опустим перпендикуляр КМ на гипотенузу АВ .
КМ ⊥АВ. Тогда ΔАМК - прямоугольный.
По условию АК =20 см, КМ =10 см. Так как катет равен половине гипотенузы, то он лежит напротив угла в 30°.
Тогда ∠КАМ = 30 °. Если АК - биссектриса ∠А, то ∠САК =∠КАМ = 30°.
∠АКВ - внешний угол треугольника ΔАСК .
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
∠АКВ= ∠С + ∠САК;
∠АКВ=90° + 30° = 120°.
Значит, градусная мера угла ∠АКВ равна 120 °.
#SPJ1