Предмет: Алгебра,
автор: veronikamila65
Положительный ряд, исследовать на сходимости ○○ Еn=1 an
Приложения:
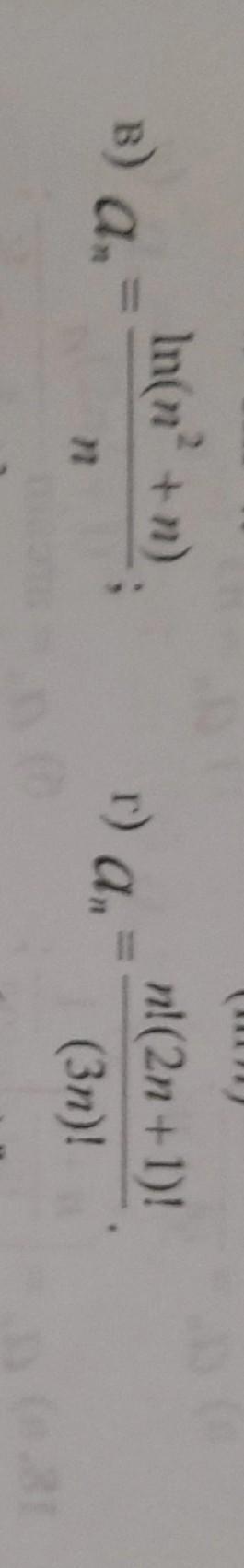
Ответы
Автор ответа:
1
Объяснение:
в)
Применим сравнительный метод. В качестве сравнения можно
выбрать ряд: . Так как aₙ≥bₙ ⇒ если ряд bₙ - расходится,
то будет расходиться и ряд аₙ. ⇒
Исследуем сходимость ряда bₙ при помощи интегрального признаки сходимости Коши:
Ряд расходится ⇒ расходится и исследуемый ряд.
Ответ: ряд расходится.
г)
Используем признак Даламбера:
(q<1 - ряд сходится, q>1 - ряд расходится).
Ответ: ряд сходится.
veronikamila65:
спасибо большое
а можно скриншот
и на другой вопрос тоже посмотрите пожалуйста
вы здесь?
sangers
В первой задаче можно было сравнить с гармоническим рядом
В первой задаче нужно проверить монотонность функции - иначе признак не работает
Похожие вопросы
Предмет: История,
автор: tokobaevnurislam4
Предмет: Алгебра,
автор: PrefectX
Предмет: Математика,
автор: alexgrynyk290311
Предмет: Алгебра,
автор: gruzdevochka
Предмет: Қазақ тiлi,
автор: asemaabilda01