помогите пожалуйста с алгеброй
является ли функция f непрерывной в точках, x1=0 и x2 =- 1, если с таблицей пожалуйста
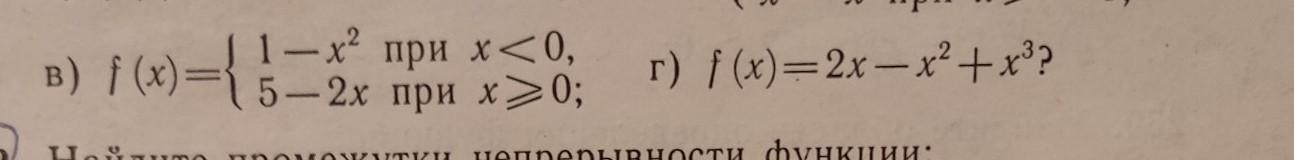
Ответы
Ответ:
в) в точке х₂ = -1 функция будет непрерывной, в точке х₁ = 0 - разрыв.
г) функция непрерывна на всей числовой оси, включая данные точки.
Объяснение:
Является ли функция f(x) непрерывной в точках, x₁=0 и x₂ =- 1.
в)
Каждая из функций 1-х² и 5-2х непрерывны на всей числовой оси. В том числе и на заданных промежутках.
Точка х₂ = -1 ∈ f(x) = 1-x² ⇒ в данной точке функция будет непрерывной.
Разрыв возможен в точке х₁=0.
Проверим функцию в этой точке:
f(0-0) = 1-0² = 1 (слева f(x) = 1-x²)
f(0+0) = 5-2·0 = 5 (справа функция f(x) = 5 - 2x)
1 ≠ 5 ⇒ функция непрерывна во всех точках, кроме х = 0. Здесь имеет место разрыв, скачок от 1 к 5.
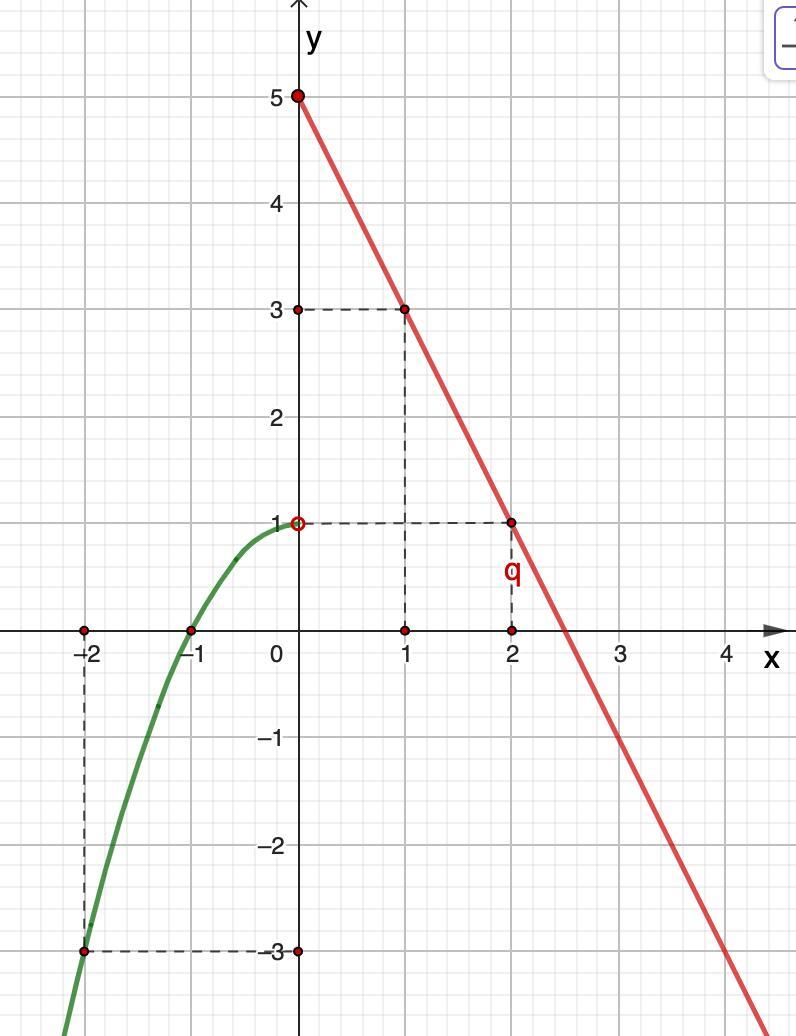
Подтвердим решение графиком.
1) f(x) = 1-x²
- квадратичная функция, график - парабола, ветви вниз.
По условию x<0. То есть, искомый график - ветвь параболы, расположенная слева от х = 0.
Точка (0; 1) будет выколота.
2) f(x) = 5 - 2x
- линейная функция, график - прямая.
Этот график расположен правее х = 0.
Для построения достаточно двух точек:
Здесь точка (0; 5) закрашена, так как x ≥ 0 - неравенство нестрогое.
Строим график. Действительно в точке х = 0 - неустранимый разрыв.
г)
f(x) = 2x - x² + x³
- данная функция непрерывна на всей числовой оси.
D(y) = (-∞; +∞)
⇒ в точках х₁ = 0 и х₂ = -1 функция непрерывна.
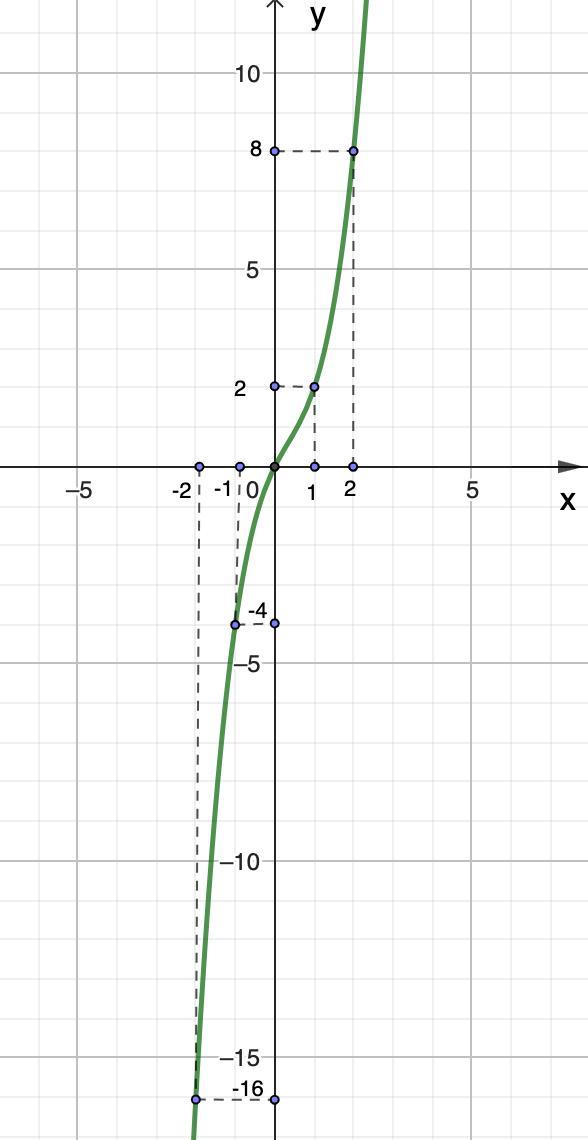
Построим график.
Строим график. Видим, что функция непрерывна на всей числовой оси.