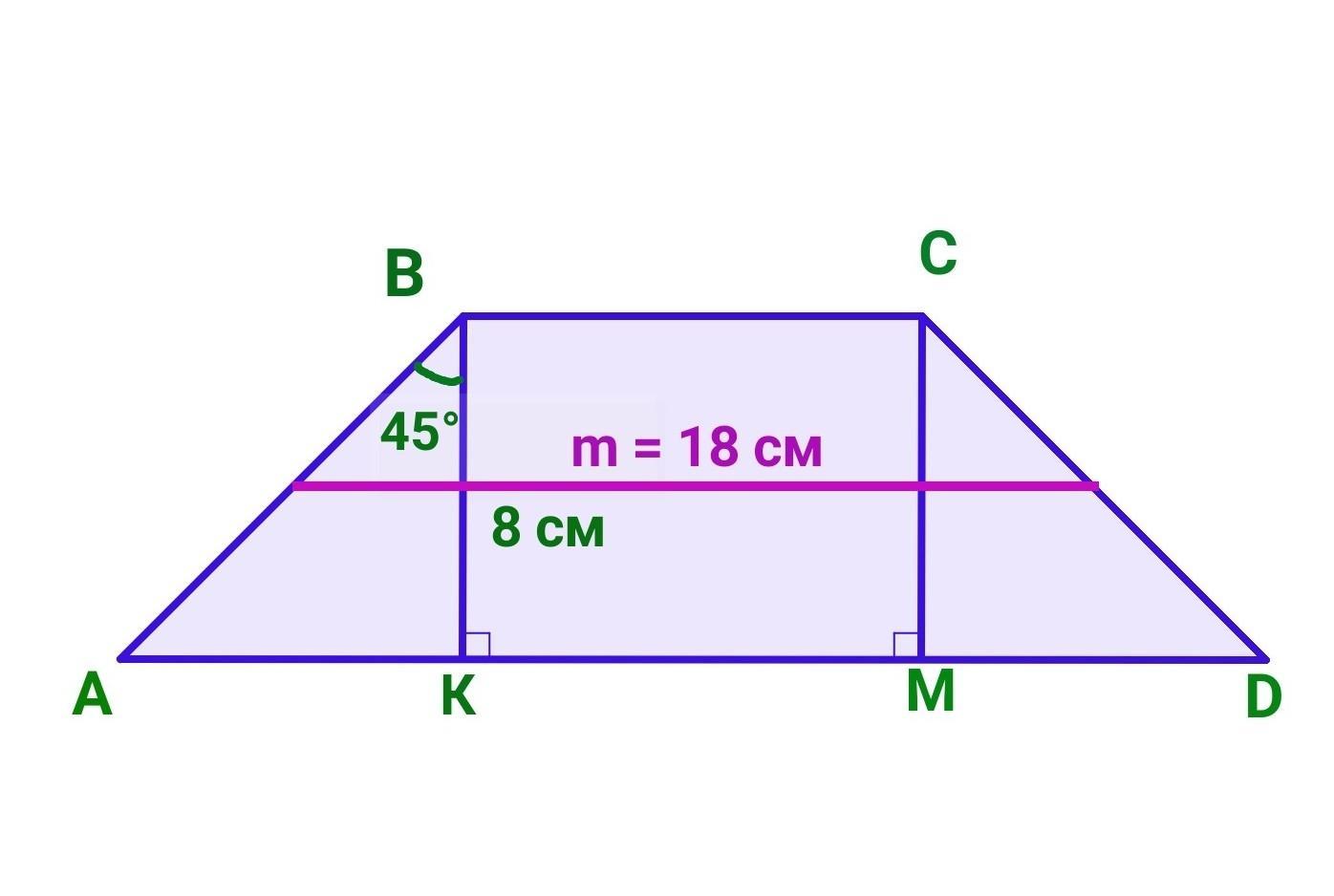
Высота равнобедренной трапеции образует с ее боковой стороной угол 45°. Найдите
основание трапеции, если ее высота 8 см, а средняя линия 18 см.
Ответы
Ответ:
Основания трапеции равны 10 см и 26 см.
Объяснение:
Высота равнобедренной трапеции образует с ее боковой стороной угол 45°. Найдите
основания трапеции, если ее высота 8 см, а средняя линия 18 см.
В равнобедренной трапеции ABCD проведем высоты ВК и СМ. Получим прямоугольник ВСМК и два равных прямоугольных треугольника : △АВК=△DCM (по гипотенузе и катету), так как АВ=DC - как боковые стороны равнобедренной трапеции, BK= CM - как её высоты.
Известно, что ВК= 8 см, ∠АВК=45°, средняя линия трапеции m=18 см.
1) Рассмотрим △АВК(∠К=90°)
Так как сумма острых углов прямоугольного треугольника равна 90°, то:
∠ВАК=90°-∠АВК=90°-45°=45° ⇒ △АВК - равнобедренный с основанием АВ.
АК=ВК=8 (см) - как боковые стороны равнобедренного треугольника.
DM= AK= 8(см) - как соответствующие стороны равных треугольников.
2) Обозначим основание ВС за х, тогда КМ=ВС=х, как противоположные стороны прямоугольника ВСМК.
AD=AK+KM+MD=8+x+8=16+x (см)
3) Длина средней линии трапеции равна полусумме оснований:
m=½•(BC+AD)
Решим уравнение:
½•(х+16+х)=18
2х+16=36
2х= 20
х=10.
Таким образом: ВС=10 (см), AD=16+10=26(см)
Ответ: 10 см, 16 см.