Розв'яжіть систему рівнянь 3xy + x = 10, |3xу + у = 12. СРОЧНО
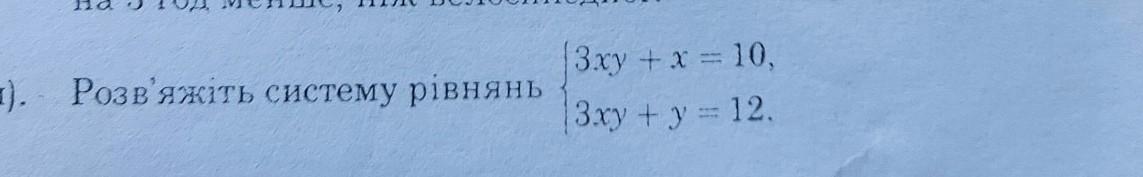
Ответы
Дана система уравнений:
$$\begin{cases}3xy+x=10 \ |3xy+y|=12 \end{cases}$$
Для удобства, рассмотрим второе уравнение в двух случаях, в зависимости от знака выражения $3xy+y$:
$$\begin{cases}3xy+x=10 \ 3xy+y=12 \quad \text{или} \quad 3xy+y=-12\end{cases}$$
Если $3xy+y=12$, то $y(3x+1)=12$. Решая это уравнение относительно $y$, получаем $y=\frac{12}{3x+1}$.
Подставляя это значение $y$ в первое уравнение, получаем:
$$3x \cdot \frac{12}{3x+1}+x=10$$
$$\Rightarrow 36x+10x+1=30x+10$$
$$\Rightarrow 6x=-9$$
$$\Rightarrow x=-\frac{3}{2}$$
Тогда $y=\frac{12}{3x+1}=-\frac{8}{3}$.
Если $3xy+y=-12$, то $y(3x+1)=-12$. Решая это уравнение относительно $y$, получаем $y=\frac{-12}{3x+1}$.
Подставляя это значение $y$ в первое уравнение, получаем:
$$3x \cdot \frac{-12}{3x+1}+x=10$$
$$\Rightarrow -36x+10x+1=30x+10$$
$$\Rightarrow -36x+10x-30x=9$$
$$\Rightarrow -56x=9$$
$$\Rightarrow x=-\frac{9}{56}$$
Тогда $y=\frac{-12}{3x+1}=\frac{24}{17}$.
Таким образом, решениями системы являются пары чисел $\left(-\frac{3}{2},-\frac{8}{3}\right)$ и $\left(-\frac{9}{56},\frac{24}{17}\right)$.