Дана функция у = x²-3x+3/x-2
а) производную функции:.
b) критические точки функции:
c) промежутки возрастания и убывания функции.
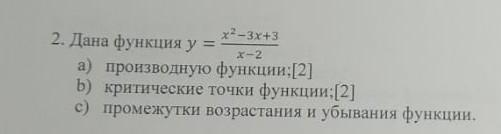
Ответы
Дана функция y = (x²-3x+3)/(x-2).
a) Чтобы вычислить производную этой функции можно воспользоваться правилом дифференцирования частного: (u/v)’ = (u’v - uv’)/v². Пусть u = x²-3x+3 и v = x-2. Тогда u’ = 2x - 3 и v’ = 1. Следовательно, производная функции y равна y’ = ((2x - 3)(x - 2) - (x²-3x+3))/((x-2)²) = (-x² + 4x - 5)/((x-2)²).
b) Критическими точками функции являются точки, в которых производная равна нулю или не существует. Производная не существует при x=2, так как знаменатель равен нулю. Решая уравнение (-x² + 4x - 5)/((x-2)²)=0 получаем x=5/2.
c) Чтобы найти промежутки возрастания и убывания функции можно воспользоваться знаком производной на промежутках между критическими точками. При x<5/2 производная отрицательна и функция убывает. При x>5/2 производная положительна и функция возрастает.