Предмет: Геометрия,
автор: dinochkaaoaoao
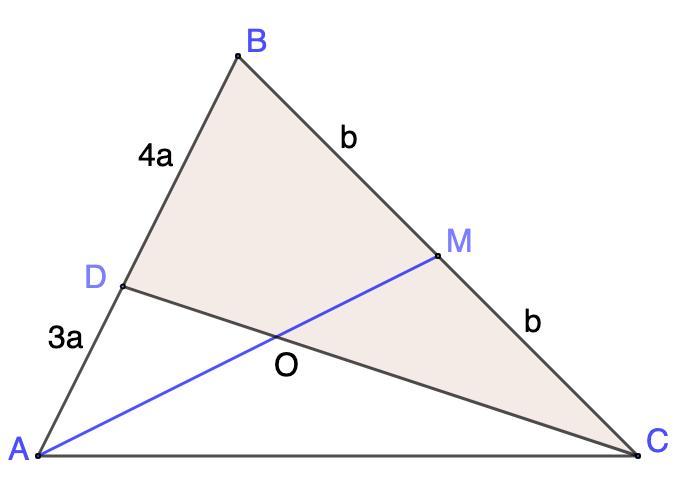
Задан треугольник АВС, из вершины А которого проведена медиана АM. На стороне AB отметили точку D так, что AD : DB = 3:4. B
каком отношении медиана АМ делит отрезок CD? Решите задачу, используя теорему Менелая.
Ответы
Автор ответа:
2
Ответ:
Медиана АМ делит отрезок CD в отношении 7 : 3.
Объяснение:
Задан треугольник АВС, из вершины А которого проведена медиана АM. На стороне AB отметили точку D так, что AD : DB = 3:4. B каком отношении медиана АМ делит отрезок CD?
Решите задачу, используя теорему Менелая.
Дано: ΔАВС;
АМ - медиана;
D ∈ AB; AD : DB = 3 : 4.
Найти: в каком отношении медиана АМ делит отрезок CD.
Решение:
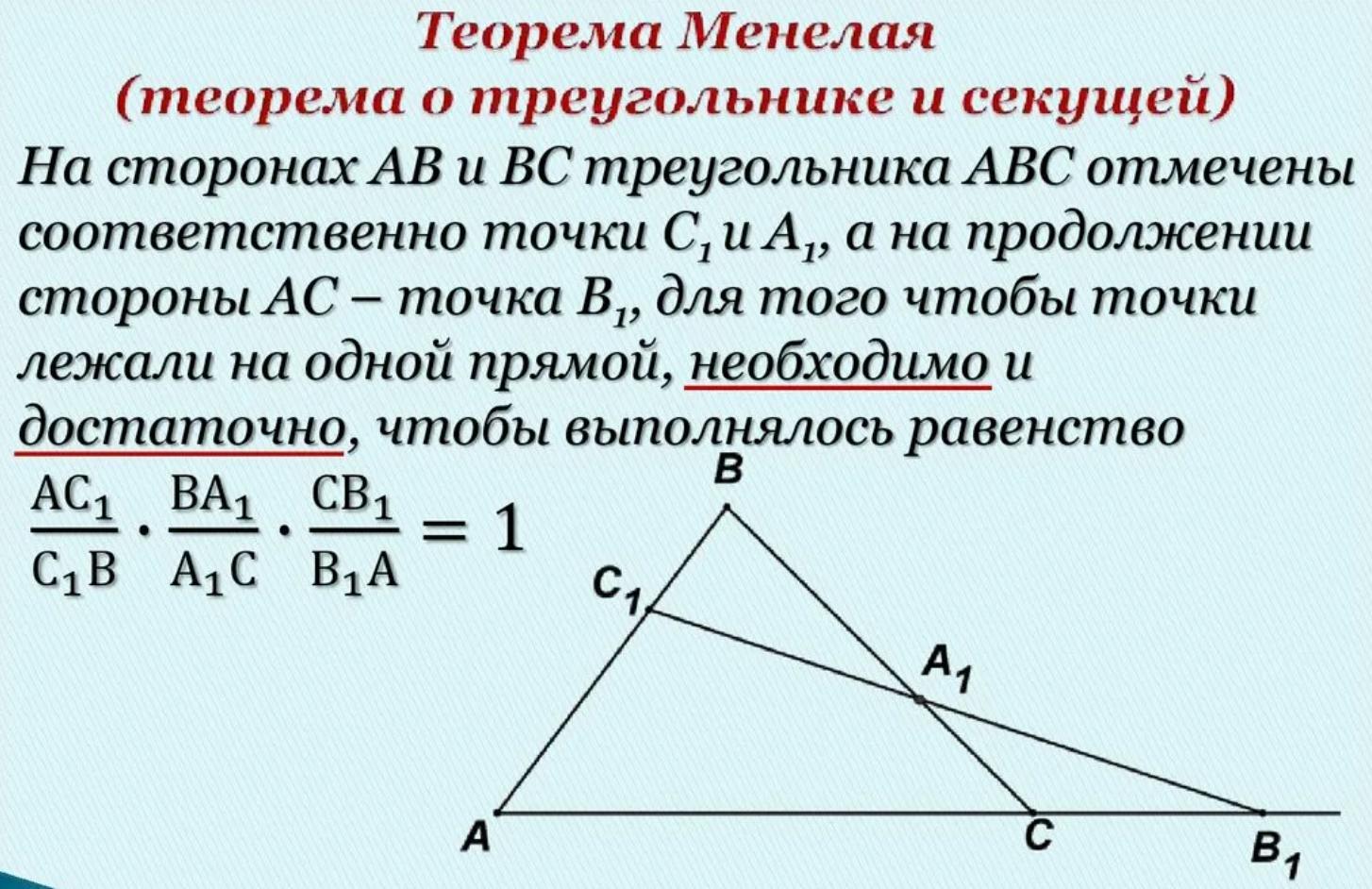
Теорему Менелая см. во вложении.
AD : DB = 3 : 4
Пусть AD = 3a, тогда DB = 4a.
АМ - медиана.
Пусть ВМ = МС = b.
Рассмотрим ΔBCD.
AM - секущая.
M ∈ BC; O ∈ DC; A ∈ BD (продолжению)
Точки M, O, A лежат на одной прямой.
⇒ справедливо равенство:
CO : OD = 7 : 3
#SPJ1
Приложения:
Похожие вопросы
Предмет: Химия,
автор: aksenenkoula65
Предмет: Қазақ тiлi,
автор: ansargajsin0
Предмет: Литература,
автор: votetopapavarot
Предмет: Химия,
автор: sashamk12345