Предмет: Геометрия,
автор: wntss252
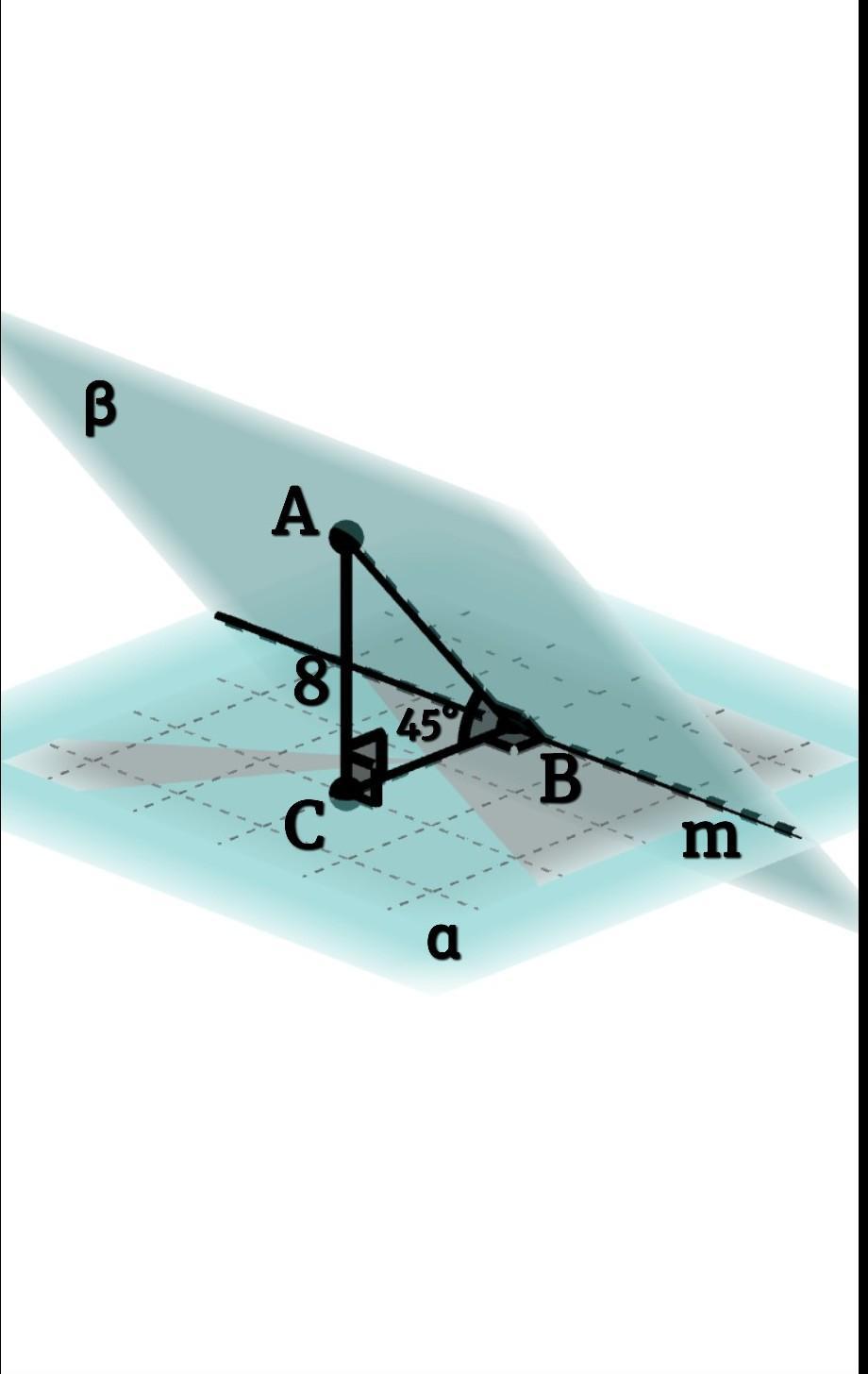
Точка A принадлежит одной из граней двугранного угла и удалена от другой грани на 8 см. Найдите расстояние от точки A до ребра двугранного угла, если величина этого угла равна 45°.
+ чертёж пожалуйста.
Ответы
Автор ответа:
4
Ответ:
AB = 8√2 см
Объяснение:
Дано: А ∈ β, Р(А;α) = 8см, ∠АВС = 45°
Найти: Р(А;m)
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение
- Расстояние от точки до плоскости - это перпендикуляр, опущенный из данной точки на плоскость. Опустим перпендикуляр АС на плоскость α. Р(А;α) = АС = 8см. Р(А;m) = AB
- Градусная мера двугранного угла равна градусной мере соответствующего ему линейного угла, который является углом между перпендикулярами к ребру двугранного угла. Опустим перпендикуляры АВ и ВС на ребро двугранного угла. Угол между ними и есть линейный угол двугранного угла, следовательно ∠АВС = 45°.
- Т.к. АС ⟂ α, СВ ∈ α ⇒АС⟂СВ. Следовательно ∆АВС - прямоугольный.
- Найдем гипотенузучерез синус угла. Синус угла - это отношение противолежащего катета(АС) к гипотенузе(АВ)
⠀⠀⠀sin45° = AC/AB
⠀⠀⠀√2/2 = 8/AB
⠀⠀⠀AB = (2*8)/√2
⠀⠀⠀AB = 16/√2 * √2/√2
⠀⠀⠀AB = 16√2/2 = 8√2(см)
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: plagiad95
Предмет: Математика,
автор: quseynqasanov567
Предмет: Английский язык,
автор: oleksandraisenko947
Предмет: Русский язык,
автор: DilanMoormeier
Предмет: Геометрия,
автор: daniilrengac6