Question

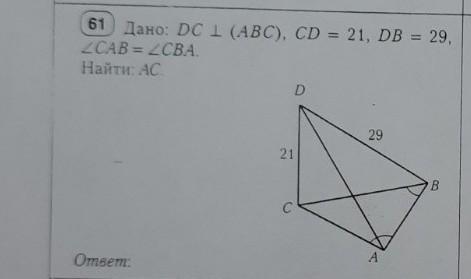
Дано:DC перпендикулярно ABC,CD=21,DB=29,угол CAB=угол CBA.Найти:AC.​

Answer 1

Ответ:

АС = 20(ед)

Объяснение:

• В плоскости основания лежит равнобедренный треугольник. Т.к. углы при основании равны.
• Если прямая перпеликулярна некой плоскости, то она перпендикулярна всем прямым, лежащим в данной плоскости. DC ⟂ (ABC)(по условию), ВС ∈ (АВС) ⇒ DC⟂BC, следовательно ∆DCB - прямоугольный. Катет ВС согласно Т.Пифагора равен: BC = √(BD²-CD²) = √(29²-21²) = √(841-441)=√400 = 20. А т.к. ∆АВС - равнобедренный, то АС = ВС = 20(ед) - как боковые стороны равнобедренного треугольника.

#SPJ1