Предмет: Алгебра,
автор: ADHpepo
Решить с помощью sinx+cosx=t
Приложения:
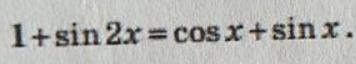
Ответы
Автор ответа:
0
Ответ:
Решаем уравнение с помощью замены
Выразим sin2x через t .
Уравнение примет вид: .
или можно записать так :
Ответ: .
Похожие вопросы
Предмет: Другие предметы,
автор: natalialastovka5
Предмет: Математика,
автор: Аноним
Предмет: Другие предметы,
автор: artemrabinin346
Предмет: Английский язык,
автор: samira1708
Предмет: История,
автор: anna14764