Внимание, очень сложная задача! Даже моим преподавателям очень тяжело в ней разобраться.
Рассмотрим систему из трех взаимодействующих кубитов, описываемых гамильтонианом Хейзенберга:
(ФОТО)
где $\vec{\sigma}i$ - вектор Паули для i-го кубита, $J{ij}$ - константы взаимодействия между кубитами, $h_i$ - константы поля вдоль оси $z$.
Требуется найти энергетический спектр этой системы и соответствующие ему собственные векторы.
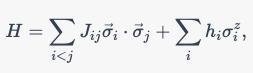
Ответы
Ответ:
Для нахождения энергетического спектра системы из трех взаимодействующих кубитов нужно решить уравнение Шредингера для данного гамильтониана:
$$H = \sum_{i=1}^3 h_i \sigma_{i,z} + \sum_{i<j} J_{ij} (\sigma_{i,x} \sigma_{j,x} + \sigma_{i,y} \sigma_{j,y} + \sigma_{i,z} \sigma_{j,z})$$
Так как система состоит из трех кубитов, то размерность гамильтониана равна $2^3 \times 2^3 = 64$, что делает аналитическое решение задачи крайне трудным. Однако можно применить численные методы для нахождения энергетического спектра и собственных векторов.
Для этого необходимо сначала перейти к базису, в котором гамильтониан имеет блочно-диагональный вид. Это можно сделать, используя преобразование Характеристического уравнения Боголюбова (ХУБ), которое позволяет свести гамильтониан к диагональному виду с помощью унитарного преобразования.
Затем можно численно решить уравнение Шредингера для каждого блока диагонализированного гамильтониана и получить энергетический спектр системы и соответствующие ему собственные векторы.
Таким образом, для решения данной задачи необходимо использовать численные методы, так как аналитическое решение крайне сложно.
Did you decide that on your own?