Question

Прошу помочь с задачкой геометрии.

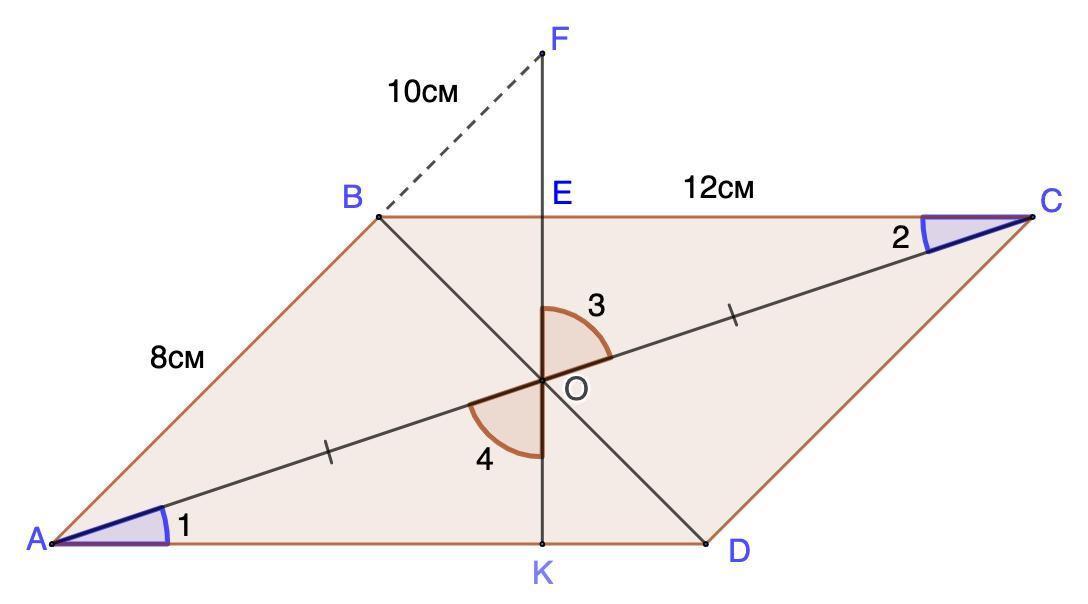
Через точку перетину діагоналей паралелограма ABCD перпендикулярно до сторони BC проведено пряму, яка перетинає BC в точці E, а продовження сторони AB - у точці F. Знайти відрізок BE, якщо AB=8 см, EC=12 см, BF=10 см

Answer 1

Ответ:

Отрезок ВЕ равен $\displaystyle \bf 6\frac{2}{3}$  см.

Объяснение:

Через точку пересечения диагоналей параллелограмма ABCD перпендикулярно стороне BC проведена прямая, которая пересекает BC в точке E, а продолжение стороны AB - в точке F. Найти отрезок BE, если AB=8 см, EC=12 см, BF=10 см.

Дано: ABCD - параллелограмм;

АС ∩ BD = O;

ОЕ ⊥ ВС;

OE ∩ AB = F

AB=8 см, EC=12 см, BF=10 см.

Найти: ВЕ.

Решение:

1. Рассмотрим ΔАОК и ΔСОЕ.

• Диагонали параллелограмма точкой пересечения делятся пополам.

⇒ АО = ОС;

∠1 = ∠2 (накрест лежащие при BC || AD и секущей АС)

∠3 = ∠4 (вертикальные)

ΔАОК = ΔСОЕ (по стороне и двум прилежащим углам, 2 признак)

⇒ ЕС = АК = 12 см (как соответственные элементы)

2. Рассмотрим ΔBFE и ΔАFК.

∠F - общий;

∠FАK = ∠FBE (соответственные при ВС || AD и секущей AF)

ΔBFE ~ ΔАFК (по двум углам)

Запишем отношение соответственных сторон:

$\displaystyle \bf \frac{BF}{AF} =\frac{BE}{AK}\\ \\\frac{10}{8+10}=\frac{BE}{12} \\\\BE=\frac{10\cdot12}{18}=\frac{20}{3}=6\frac{2}{3}$  (см)

Отрезок ВЕ равен $\displaystyle \bf 6\frac{2}{3}$  см.