Question

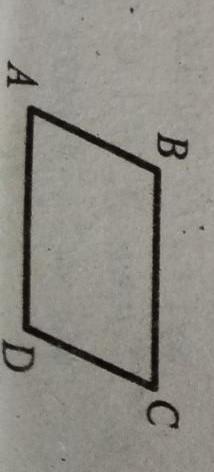
На рисунку 255 ВС \\ АD , ВС=АD. Доведіть ,що АВ=CD​

Answer 1

Відповідь:

Для доведення рівності АВ=CD необхідно та достатньо показати, що трикутники АВС і СДВ є подібними.

З рисунку знаємо, що:

ВС = АD

ВС // АD (оскільки ВС і АD лежать на паралельних прямих ВС та АD)

АВ = АС (оскільки трікутник АВС рівнобедрений, а тому АВ=АС)

З цього випливає, що кут ВАС дорівнює куту СДВ (оскільки вони спираються на паралельні прямі).

Отже, маємо наступне подібність трикутників:

трикутник АВС підібний трикутнику СДВ за спільним кутом (кут ВАС дорівнює куту СДВ) і спільною стороною ВС.

З підібності трикутників випливає, що співвідношення між відповідними сторонами дорівнює співвідношенню між відповідними сторонами іншого трикутника. Зокрема,

АВ/ВС = СД/ВС,

або, еквівалентно,

АВ = СД.

Отже, АВ=CD, як і потрібно було довести.

Пояснення: