Предмет: Алгебра,
автор: alianna15
Очислити ігтеграл.
Потрібний 3 приклад
Приложения:
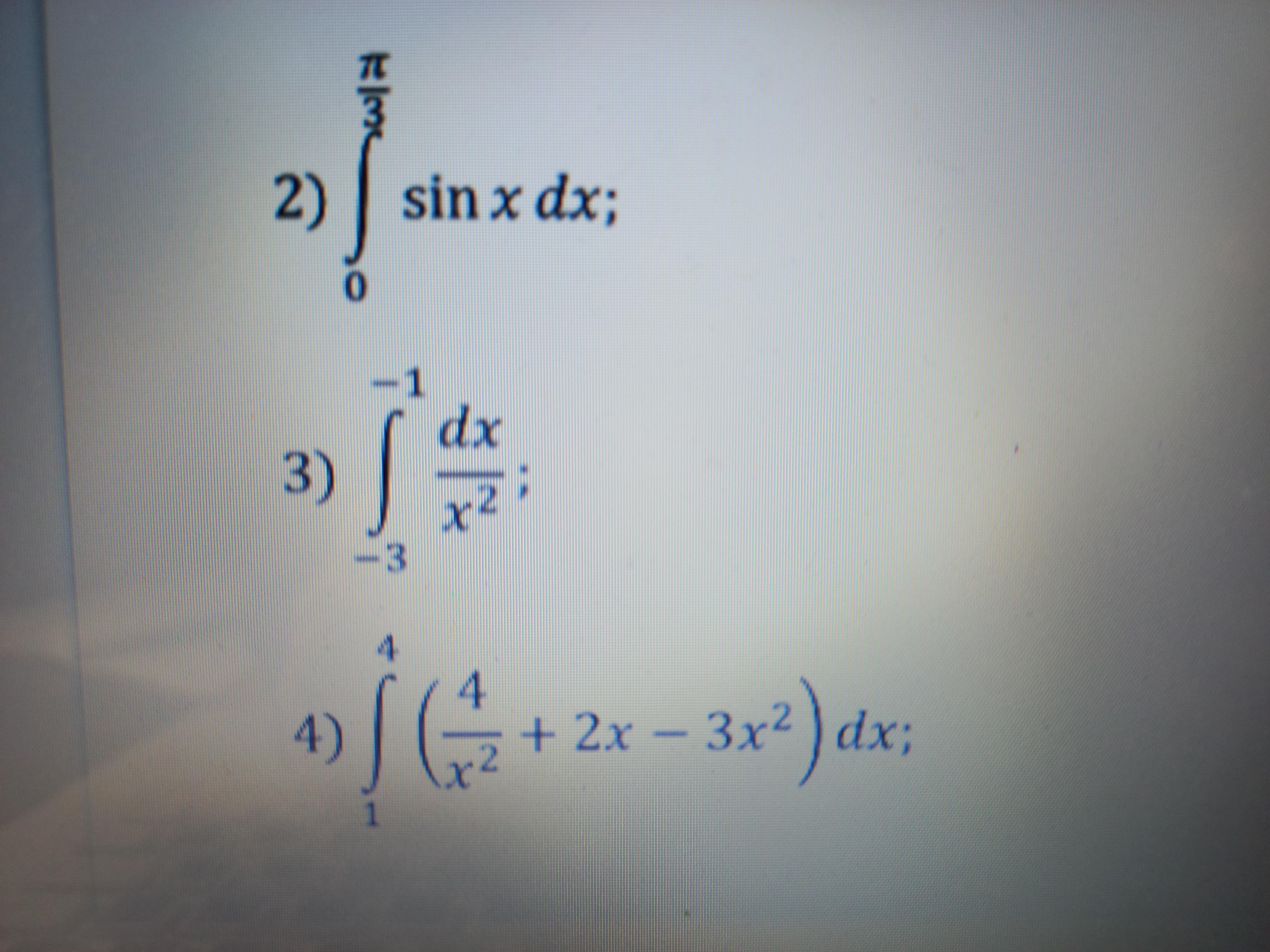
Ответы
Автор ответа:
0
Ответ:
2)
3)
4)
Объяснение:
Вычислить интеграл.
Формулы:
Формула Ньютона-Лейбница:
2)
3)
4)
Похожие вопросы
Предмет: Українська мова,
автор: vika228kika
Предмет: Математика,
автор: solk4206
Предмет: Русский язык,
автор: salimabaku
Предмет: Геометрия,
автор: gdanastasia
Предмет: Геометрия,
автор: Sivakatya