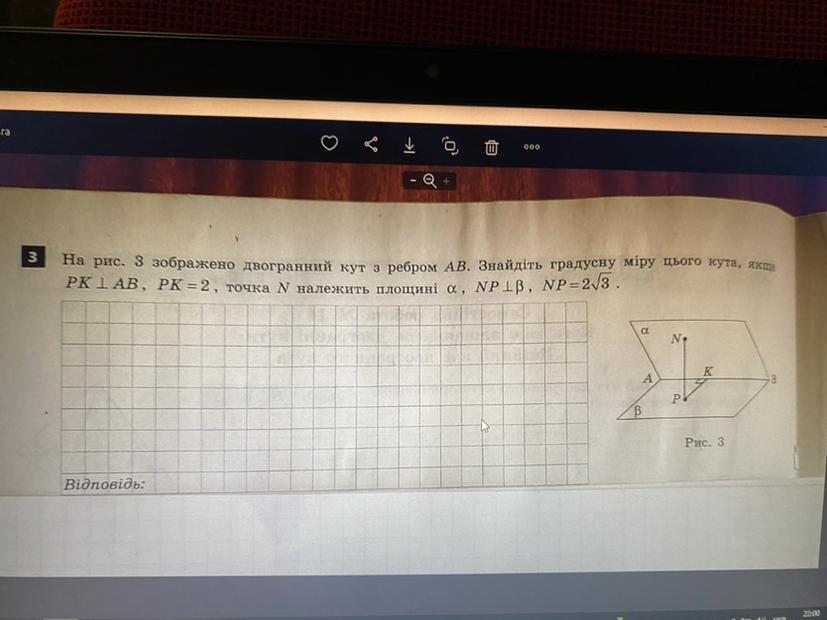
На рис. 3 зображено двогранний кут з ребром АВ. Знайдіть градусну міру цього кута, якщо
PК|AB, РК = 2, точка N належить площині a , NP | B, NP - 2/3 .
Ответы
Ответ:
дай коронку если не сложно)
Объяснение:
На рис. 3 зображено двогранний кут з ребром АВ. Знайдіть градусну міру цього кута, якщо
PК|AB, РК = 2, точка N належить площині a , NP | B, NP - 2/3 .
За умовою, ми знаємо, що РК паралельно ребру АВ, тому ми можемо вважати, що РК перетинає площину АВС в точці К і утворює кут АКР.
Також за умовою ми знаємо, що точка N належить площині АВС і лежить на прямій, паралельній ребру АВ, тобто NP || AB.
Отже, точки А, Р, К і N лежать на одній площині.
За теоремою Піфагора у прямокутному трикутнику АПК знаходимо довжину ПК:
PK^2 = AP^2 + AK^2 = 1^2 + 2^2 = 5
PK = sqrt(5)
Так як А, Р і К лежать на одній прямій, то градусна міра кута АКР дорівнює сумі градусних мір кутів АКП і РКП.
Також з умови ми знаємо, що NP - 2/3, а NP || B. Оскільки точка Р лежить на прямій АК і на площині АВС, то вона також лежить на прямій, паралельній ребру ВС. Отже, висота NP проходить через середину ребра ВС, тому NP дорівнює половині довжини ВС:
NP = 1/2 * BC = 1/2 * 3 = 3/2
Також за теоремою Піфагора в прямокутному трикутнику НРК знаходимо довжину РН:
RN^2 = PK^2 + NP^2 = 5 + (3/2)^2 = 31/4
RN = sqrt(31/4) = (sqrt(31))/2
Тоді тангенс кута РКП дорівнює відношенню сторін РК і РН:
tg(∠РКП) = PK / RN = sqrt(5) / (sqrt(31)/2) = 2sqrt(5)/sqrt(31) = (2/31) * sqrt(155)
За теоремою тангенсів, градусна міра кута РКП дорівнює:
∠РКП = arctg(tg(∠РКП)) = arctg((2/31) * sqrt(155)) ≈ 11.4°
Тоді градусна міра кута АКР дорівнює:
∠АКР = ∠АКП