Предмет: Алгебра,
автор: veronikamila65
Помогите пожалуйста решить несобственные интегралы
Приложения:
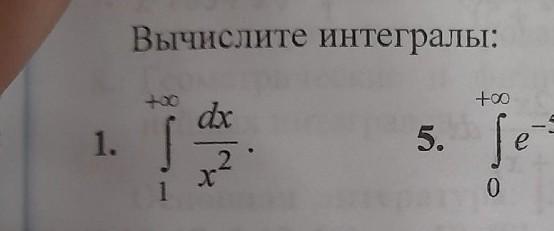
Ответы
Автор ответа:
2
Ответ:
Вычислить несобственный интеграл .
Правило (выучи) :
.
Так как получили , что несобственный интеграл равен числу, то несобственный интеграл сходится .
- табличный интеграл
Приложения:

veronikamila65:
спасибо большое
а можете пожалуйста скриншот добавить, извините что каждый раз прощу
спасибо большое
вы лучшая
еще один вопрос остался, и на это помогите и все , пожалуйста)
Похожие вопросы
Предмет: Українська мова,
автор: kovaljulia422
Предмет: Информатика,
автор: Sonatakira
Предмет: Физика,
автор: illyapon666
Предмет: Химия,
автор: viktoriashablienko
Предмет: Алгебра,
автор: idel655