СРОЧНО ДАЮ МНОГО БАЛЛОВ
Бросают две игральные кости. Событие K — «на первой кости выпало четное число очков». Событие L — «на второй кости выпало четное число
очков».
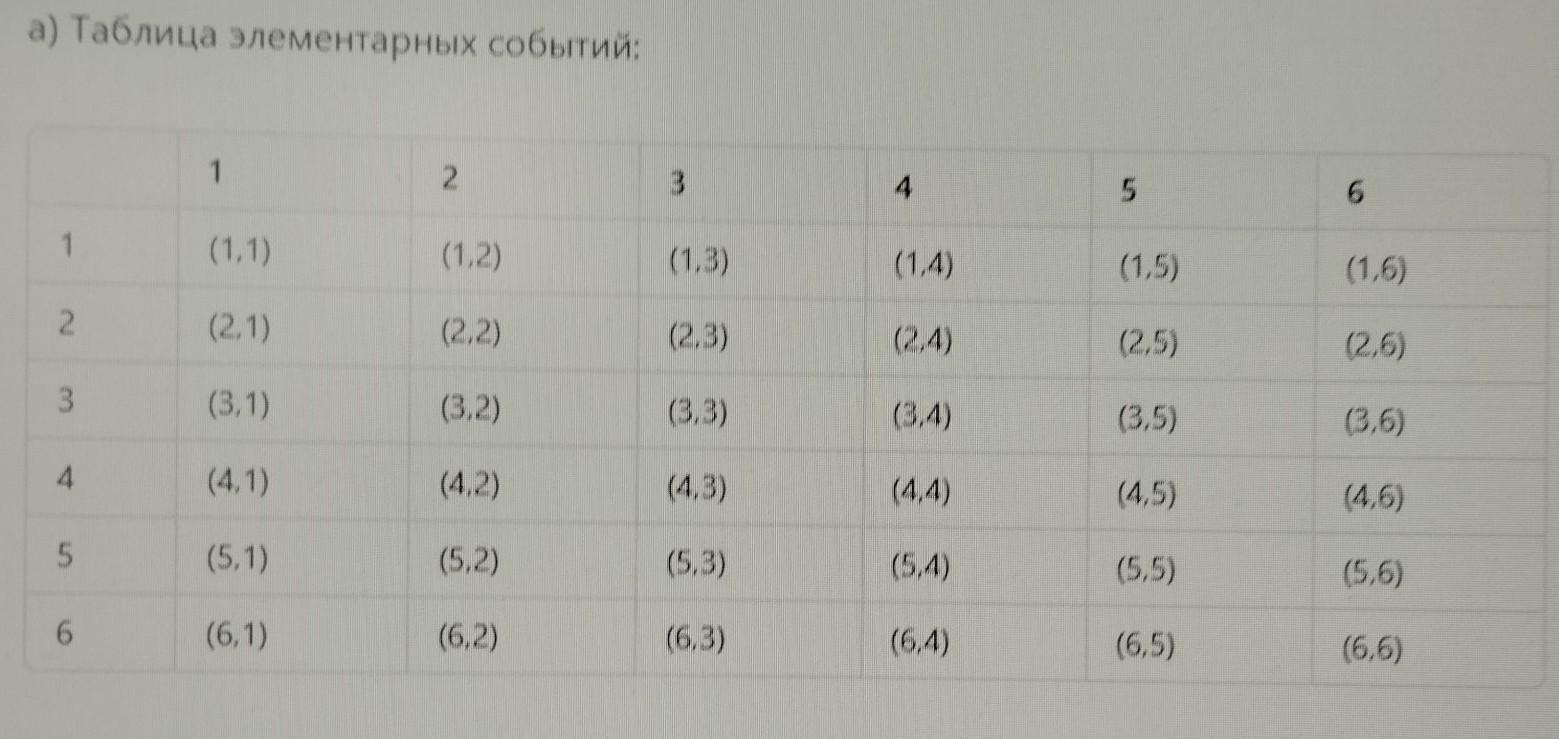
а) Выделите в таблице элементарных событий этого опыта элементарные
события, благоприятствующие событиям K и L.
б) Есть ли у событий K и L общие элементарные события? Если да, то какие
они и сколько их?
в) Опишите словами событие K ∪L.
г) Найдите вероятность события K ∪L.
Ответы
Ответ:
Таблица элементарных событий:
Объяснение:
Элементарные события, благоприятствующие событию K (на первой кости выпало четное число очков): (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6).
Элементарные события, благоприятствующие событию L (на второй кости выпало четное число очков): (1,2), (1,4), (1,6), (2,2), (2,4), (2,6), (3,2), (3,4), (3,6), (4,2), (4,4), (4,6), (5,2), (5,4), (5,6), (6,2), (6,4), (6,6).
б) Да, у событий K и L есть общие элементарные события: (2,2), (2,4), (2,6), (4,2), (4,4), (4,6), (6,2), (6,4), (6,6). Их 9 штук.
в) Событие K ∪ L означает, что на первой или второй кости выпало четное число очков, или обеих костях сразу. То есть это событие означает, что хотя бы одно из событий K или L произошло.
г) Вероятность события K ∪ L можно найти как сумму вероятностей событий K и L, за вычетом вероятности их пересечения:
P(K ∪ L) = P(K
Можно пожалуйста лучший ответ